Methoden Einführung: Statistik mit Löwen – Teil 3


Hauptanalyse
Unsere Archäologen stehen vor ihrem analytischen Ziel, die Voraussetzungsprüfung der ANOVA ist überstanden. Zur Erinnerung noch einmal die Forschungsfrage:
H1: Je länger die Löwen bei den Zirkusspielen im Einsatz sind, desto höher ist ihr Gewicht.
Da alle Daten (Gewicht als metrische und Monate im Zirkus als kategoriale Variable) vorbereitet sind, kann es direkt losgehen. Der Stata-Befehl für die Analyse ist:
anova gewicht monate_kat
und erzeugt die untenstehenden Ergebnisse.

Insgesamt liegen N = 517 Fälle für die Analyse vor, der erklärte Varianzanteil beträgt $R^2$ = 0.7505 = 75.05%. Die kategorisierten Monate können also einen sehr hohen Varianzanteil am Gewicht erklären. Darunter folgt eine Zeile für Model und eine Zeile für die Monate. Beide Zeilen sind in diesem einfachen Modell gleich was die Werte angeht (SS steht für Sum of Squares). Für Nutzer von SPSS sei an dieser Stelle gesagt, dass hier nur eine der beiden Zeilen aufgeführt wird und mit „zwischen den Gruppen“ (engl.: between groups) beschriftet ist. Vor allem der englische Begriff ist in der statistischen Fachwelt sehr gebräuchlich und hätte von Stata auch verwendet werden sollen. Die Zeile „residuals“ wird bei SPSS „innerhalb der Gruppen“ (eng.: within groups) genannt, auch hier ist der englische Fachbegriff durchaus in deutscher Fachliteratur üblich.
Zusätzlich findet sich beim between-Effekt die Angabe des F-Werts sowie der dazu gehörende Signifikanzwert. Dieser ist mit $p le .001$ signifikant, so dass die Monate im Zirkus einen signifikanten Effekt auf das Gewicht haben. Eine Aussage darüber, welche Kategorien der Monate hier genau signifikant sind und welchen Unterschied diese bezüglich des Gewichts haben, kann an dieser Stelle noch nicht getroffen werden. Dokumentiert wird das Ergebnis der ANOVA mit F(df1,df2) = F-Wert, p-Wert. In unserem Fall also mit F(5,511) = 311.49, $p le .001$.
In einigen Fachbereichen ist es üblich die Effektstärke der Analyse mit anzugeben. Ohne auf die Bedeutung dieser Maßzahl näher einzugehen, sei hier kurz gesagt, dass eine Effektstärke eine Aussage darüber trifft, ob ein gefundener Zusammenhang einer Analyse auch eine praktische Relevanz besitzt. Für die ANOVA lässt sich $eta^2$ als Effektstärke einfach berechnen:
$eta^2 = frac{ SS_{between} }{ SS_{top} } = frac{415662.19} {552039.08} = 0.753$
In einer einfaktoriellen Varianzanalyse wie dieser lässt sich $eta^2$ einfach mit 100 multiplizieren, und es gilt:
$R^2 = eta^2$
Somit lässt sich die Interpretation von $eta^2$ ebenso einfach auf den Korrelationskoeffizienten r herunterbrechen, welcher einfach mit
$r = sqrt{R^2} = 0.868$
zu berechnen ist (Field 2013: 472). Auch hier zeigt sich der extrem starke Effekt der ANOVA. Stata kann die Effektstärke auch direkt nach der ANOVA berechnen, dafür muss folgender Befehl verwendet werden
estat esize
Da $eta^2$ mathematisch einen Bias aufweist (Levine 2002), wird meist Omega-Quadrat als Maß der Effektstärke für eine ANOVA angegeben. Stata kann dies mittlerweile von Haus aus berechnen mit
estat esize, omega
Das Ergebnis ist $omega^2 = 0.7502$, hinsichtlich der Grenzwerte gelten die gleichen wie für $eta^2$ (Kirk 1996). Es liegt also ein starker Effekt vor. Doch wie unterscheiden sich nun die Monate im Detail?
posthoc-Test
Zur Erinnerung wie schwer die Löwen durchschnittlich in den einzelnen Monatskategorien sind, wird die Tabelle aus Teil 2 an dieser Stelle noch einmal gezeigt.

Stata bietet im Nachgang der ANOVA mehrere posthoc Befehle an. Mit
pwcompare monate_kat, group effects mcompare(bon)würden alle Monatskategorien, d.h. alle möglichen Kombinationen, miteinander verglichen werden. Dies erzeugt eine recht große Tabelle, die hier nicht abgebildet wird, da sie für uns nicht von Interesse ist. Da es das Ziel der Forscher war zu untersuchen, ob mit längerem Aufenthalt die Löwen bei den Zirkusspielen an Gewicht zunehmen, interessiert uns im Moment nur, ob Löwen, die in der nächsthöheren Kategorie von Monaten sind, sich gegenüber der vorherigen Kategorie unterscheiden. Der Befehl „pwcompare“ kann uns hier jedoch nicht weiterhelfen, so dass wir nunmehr
contrast ar.monate_kat, mcompare(bon) effectsdurchführen müssen. Mit der Präfix “ar.” weisen wir Stata an, beginnend mit der ersten Kategorie (weniger als 6 Monate) immer zur nächsthöheren Kategorie zu vergleichen. Die Ergebnisse sind in der unten stehenden Tabelle zu finden.
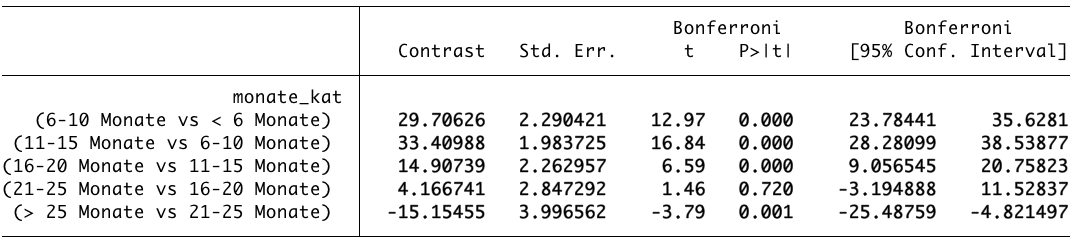
Die Kategorie „6-10 Monate“ unterscheidet sich von der Kategorie „$le$ 6 Monate“ um 29.71. Der Kontrast ist dabei nichts anderes als die Differenz der Mittelwerte dieser Kategorien, also 131.17 – 101.46 = 29.71. Dabei wird immer die zuletzt genannte Kategorie des Kontrasts von der zuerst genannten Kategorie abgezogen. Da der Wert positiv ist, bedeutet dies also, dass die Löwen mit 6-10 Monaten im Zirkus durchschnittlich 29,71kg schwerer sind als Löwen die weniger als 6 Monate im Zirkus sind. Dieses Ergebnis ist mit t = 12.97, $p le .001$ signifikant. Als posthoc Test wurde Bonferroni durchgeführt. Eine Diskussion der unzähligen Tests kann an dieser Stelle nicht gegeben werden und es sei an dieser Stelle auf weiterführende Fachliteratur verwiesen (Field 2013: 458 ff.). Auch wenn Bonferroni recht konservativ rechnet, so kann mit Blick auf diese Analyse gesagt werden, dass keine andere Testmethode ein anderes Ergebnis hervorbringt.
Der Blick auf die Tabelle verrät also, dass die Löwen mit zunehmender Zahl an Monaten schwerer werden, zunächst legen sie 29.71kg ($p le .001$) zu, dann 33.41kg ($p le .001$), die Gewichtszunahme verringert sich dann auf 14.91kg ($p le .001$) beim Vergleich von „16-20 Monate“ vs. „11-15 Monate“ und beim darauf folgenden Vergleich liegt die Zunahme lediglich bei durchschnittlich 4.17kg, ist aber mit p = .720 nicht signifikant. Im Vergleich der letzten und vorletzten Kategorie miteinander nehmen die Löwen dann wieder ab, der Kontrast liegt bei -15.15 ($p le .01$).
Mit Hilfe des komfortablen Befehls „margins“ bzw. „marginsplot“ lässt sich nun folgende Grafik zu dieser Veränderung anzeigen, wobei auf den Code, der trotz der Einfachheit der Darstellung relativ lang ist, an dieser Stelle verzichtet werden soll.

Auch wenn die obenstehende Grafik inhaltlich bereits die Wünsche der Forscher erfüllt, soll eine weitere erzeugt werden (siehe unten). Diese Grafik zeigt den Wert des Kontrasts zwischen den aufsteigenden Kategorien der Monate auf. Zusätzlich wurde ein rote Linie am Wert für 0kg abgetragen, welche einmal durch das Konfidenzintervall durchbrochen wird. Bei „21-25 vs. 16-20“ Monate ist der Kontrast +4.17kg, es liegt also noch eine leichte Gewichtszunahme vor, das Konfidenzintervall liegt jedoch zwischen -3.20 und +11.53. Mit einer 95%igen Wahrscheinlichkeit liegt der Kontrast also in diesem Bereich und umschließt den Wert 0. Das Ergebnis ist somit auch ohne den eigentlich p-Werten zu kennen, nicht signifikant, da der Kontrast anstatt positiv (+4.17kg) auch negativ sein kann (bis -3.20kg) und die inhaltliche Interpretation komplett anders wäre.

Die Forscher sehen ihre Hypothese als größtenteils bestätigt, fragen sich aber nach der ersten Euphorie, ob denn nicht das Alter der Löwen einen Nebeneffekt hat, den man statistisch Kovariate nennt und zu einer Kovarianzanalyse (ANCOVA) führt.
Referenzen
- Cohen, J. (1988): Statistical Power Analysis for the Behavioral Sciences. Hoboken: Taylor and Francis
- Field, Andy (2013): Discovering Statistics Using SPSS. 4th Edition, SAGE: London
- Kirk, R. E. (1996): Practical significance: A concept whose time has come. Educational and Psychological Measurement 56(5), S. 746-759
- Levine, T. R., & Hullett, C. R. (2002). Eta Squared, Partial Eta Squared, and Misreporting of Effect Size in Communication Research. Human Communication Research 28(4), S. 612–625


