Gemeinschaftsdetektion mit Louvain und Infomap

In meinem letzten Blogpost habe ich über Netzwerke und deren Visualisierung in R geschrieben. Für die Farbgebung der Objekte habe ich die Les Misérables-Charaktere mithilfe von Louvain, einem Community Detection Algorithmus, in mehrere Gruppen geclustert.

Community Detection Algorithmen sind nicht nur nützlich, um Charaktere in französischen Liedtexten zu gruppieren. Bei statworx nutzen wir diese Methoden, um unseren Kunden Einblicke in ihr Produktportfolio, ihre Kunden- oder Marktstruktur zu geben. In diesem Blogpost möchte ich dir die Magie hinter Community Detection zeigen und eine theoretische Einführung in die Louvain- und Infomap-Algorithmen geben.

Finde Gruppen mit hoher Dichte an Verbindungen innerhalb und niedriger Dichte zwischen Gruppen

Netzwerke sind nützliche Konstrukte, um die Organisation von Interaktionen in sozialen und biologischen Systemen zu schematisieren. Sie eignen sich ebenso gut zur Darstellung von Interaktionen in der Wirtschaft, insbesondere im Marketing. Eine solche Interaktion kann ein gemeinsamer Kauf von zwei oder mehr Produkten sein oder ein gemeinsamer Vergleich von Produkten in Online-Shops oder auf Preisvergleichsportalen.

Netzwerke bestehen aus Objekten und Verbindungen zwischen den Objekten. Die Verbindungen, auch Kanten genannt, können nach bestimmten Kriterien gewichtet werden. Im Marketing ist beispielsweise die Anzahl oder Häufigkeit gemeinsamer Käufe zweier Produkte eine sinnvolle Gewichtung der Verbindung zwischen diesen beiden Produkten. Meist sind solche realen Netzwerke so groß und komplex, dass wir ihre Struktur vereinfachen müssen, um nützliche Informationen aus ihnen zu gewinnen. Die Methoden der Community Detection helfen dabei, Gruppen im Netzwerk zu finden, mit einer hohen Dichte an Verbindungen innerhalb der Gruppen und einer geringen Dichte an Verbindungen zwischen den Gruppen.

Wir schauen uns die beiden Methoden Louvain Community Detection und Infomap an, da sie in der Studie von Lancchinetti und Fortunato (2009) die besten Ergebnisse lieferten, als sie auf verschiedene Benchmarks von Community Detection Methoden angewendet wurden.

Louvain: Baue Cluster mit hoher Modularität in großen Netzwerken

Die Louvain Community Detection Methode, entwickelt von Blondel et al. (2008), ist ein einfacher Algorithmus, der schnell Cluster mit hoher Modularität in großen Netzwerken finden kann.

Modularität

Die sogenannte Modularität misst die Dichte der Verbindungen innerhalb von Clustern im Vergleich zur Dichte der Verbindungen zwischen Clustern (Blondel 2008). Sie wird als Zielfunktion verwendet, die bei einigen Community Detection Techniken maximiert werden soll, und nimmt Werte zwischen -1 und 1 an. Im Falle gewichteter Verbindungen zwischen den Objekten können wir die Modularität mit folgender Formel definieren:

$$ Q=frac{1}{2m}sumnolimits_{p,q} [A_{pq}-frac{k_{p}k_{q}}{2m}]delta(C_{p}, C_{q}) $$

mit:

$A_{pq}$: Gewicht einer Verbindung zwischen Objekt $p$ und $q$

$k_{p}$: $sumnolimits_{q}A_{pq}$ = Summe der Gewichte aller vom Objekt $p$ ausgehenden Verbindungen

$C_{p}$: Cluster, dem das Objekt $p$ zugeordnet wurde

$delta(C_{p}, C_{q})$: Dummy-Variable, die den Wert 1 annimmt, wenn beide Objekte $p$ und $q$ demselben Cluster zugeordnet sind

$m$: $frac{1}{2}sumnolimits_{p,q} A_{pq}$ = Summe der Gewichte aller Verbindungen zwischen allen vorhandenen Objekten, geteilt durch 2

Phasen

Der Algorithmus ist in zwei Phasen unterteilt, die wiederholt werden, bis die Modularität nicht weiter maximiert werden kann. In der 1. Phase wird jedes Objekt als ein separates Cluster betrachtet. Für jedes Objekt $p$ $(p = 1, …, N)$ wird geprüft, ob sich die Modularität erhöht, wenn $p$ aus seinem Cluster entfernt und dem Cluster eines Objekts $q$ $(q = 1, …, N)$ zugewiesen wird. Das Objekt $p$ wird dann dem Cluster zugewiesen, das den größten Anstieg der Modularität bewirkt. Dies gilt jedoch nur im Fall eines positiven Anstiegs. Falls durch die Verschiebung kein positiver Anstieg der Modularität erreicht werden kann, bleibt das Objekt $p$ in seinem bisherigen Cluster. Der oben beschriebene Prozess wird wiederholt und sequentiell für alle Objekte durchgeführt, bis keine Verbesserung der Modularität mehr erreicht werden kann. Ein Objekt wird dabei häufig mehrfach betrachtet und zugewiesen. Die 1. Phase endet also, wenn ein lokales Maximum gefunden wurde, d.h., wenn keine einzelne Verschiebung eines Objekts die Modularität verbessern kann.

Aufbauend auf den in der 1. Phase gebildeten Clustern wird in der 2. Phase ein neues Netzwerk erzeugt, dessen Objekte nun die Cluster selbst sind, die in der 1. Phase gebildet wurden. Um Gewichtungen für die Verbindungen zwischen den Clustern zu erhalten, wird die Summe der Gewichtungen der Verbindungen zwischen den Objekten zweier entsprechender Cluster verwendet. Wenn ein solches neues Netzwerk mit „Metacluster“ gebildet wurde, werden die Schritte der 1. Phase im nächsten Schritt auf das neue Netzwerk angewendet und die Modularität weiter optimiert. Ein vollständiger Durchlauf beider Phasen wird als Pass bezeichnet. Solche Pässe werden wiederholt durchgeführt, bis sich keine Veränderung der Cluster mehr ergibt und ein Maximum der Modularität erreicht ist.

Infomap: Minimiere die Beschreibungslänge eines Random Walks

Die Infomap-Methode wurde erstmals von Rosvall und Bergstrom (2008) vorgestellt. Das Vorgehen des Algorithmus ist im Kern identisch mit dem Verfahren von Blondel. Der Algorithmus wiederholt die zwei beschriebenen Phasen, bis eine Zielfunktion optimiert ist. Allerdings verwendet Infomap als zu optimierende Zielfunktion nicht die Modularität, sondern die sogenannte Map Equation.

Map Equation

Die Map Equation nutzt die Dualität zwischen dem Auffinden von Clusterstrukturen in Netzwerken und der Minimierung der Beschreibungslänge der Bewegung eines sogenannten Random Walks (Bohlin 2014). Dieser Random Walker bewegt sich zufällig von Objekt zu Objekt im Netzwerk. Je stärker die Verbindung eines Objekts gewichtet ist, desto wahrscheinlicher wird der Random Walker diese Verbindung nutzen, um zum nächsten Objekt zu gelangen. Ziel ist es, Cluster zu bilden, in denen sich der Random Walker möglichst lange aufhält, d.h., die Gewichtungen der Verbindungen innerhalb des Clusters sollen größere Werte annehmen als die Gewichtungen der Verbindungen zwischen Objekten verschiedener Cluster. Die Struktur des Map-Equation-Codes ist so ausgelegt, dass sie die Beschreibungslänge des Random Walks komprimiert, wenn sich der Random Walker über längere Zeiträume in bestimmten Bereichen des Netzwerks aufhält. Daher besteht das Ziel darin, die Map Equation zu minimieren, die für gewichtete, aber ungerichtete Netzwerke wie folgt definiert ist (Rosvall 2009):

$$ L(M)=wcurvearrowright log(wcurvearrowright)-2sum_{k=1}^K w_{k}curvearrowright log(w_{i}curvearrowright)-sum_{i=1}^N w_{i}log(w_{i})+sum_{k=1}^K (w_{k}curvearrowright+w_{i})log(w_{k}curvearrowright+w_{k}) $$  

mit:

$M$: Netzwerk mit $N$ Objekten ($i = 1, ..., N$) und $K$ Clustern ($k = 1, ..., K$)

$w_{i}$: relatives Gewicht aller Verbindungen eines Objekts i, d.h. die Summe der Gewichte aller Verbindungen eines Objekts geteilt durch die Summe der Gewichte aller Verbindungen des Netzes

$w_{k}$: $sumnolimits_{iin k}w_{i}$: Summe der relativen Gewichte aller Verbindungen der Objekte des Clusters $k$

$w_{k}curvearrowright$: Summe der relativen Gewichte aller Verbindungen der Objekte des Clusters $k$, die den Cluster verlassen (Verbindungen zu Objekten aus anderen Clustern)

$wcurvearrowright$: $sum_{k=1}^K w_{k}$ = Summe der Gewichte aller Verbindungen zwischen Objekten aus verschiedenen Clustern

Diese Definition der Map Equation basiert auf der sogenannten Entropie, dem durchschnittlichen Informationsgehalt bzw. der Informationsdichte einer Nachricht. Dieser Begriff basiert auf dem Source-Coding-Theorem von Shannon aus dem Bereich der Informationstheorie (Rosvall 2009).

Das oben beschriebene Vorgehen wird im Folgenden als Hauptalgorithmus bezeichnet. Objekte, die im ersten Schritt des Hauptalgorithmus beim Erstellen des neuen Netzwerks demselben Cluster zugewiesen wurden, können in der zweiten Phase nur gemeinsam verschoben werden. Eine zuvor optimale Verschiebung in einen bestimmten Cluster muss in einem späteren Durchlauf nicht mehr unbedingt optimal sein (Rosvall 2009).

Erweiterungen

Es kann also theoretisch noch bessere Clusteraufteilungen geben als die Lösung des Hauptalgorithmus. Um die Lösung des Hauptalgorithmus zu verbessern, gibt es im Vergleich zur Louvain Community Detection zwei Erweiterungen:

Subcluster-Verschiebung: Die Subcluster-Verschiebung betrachtet jedes Cluster als eigenes Netzwerk und wendet den Hauptalgorithmus auf dieses Netzwerk an. So entsteht in jedem Cluster, im vorherigen Schritt, durch ein oder mehrere Subcluster eine optimale Partitionierung des Netzwerks. Alle Subcluster werden erneut ihrem Cluster zugewiesen und können nun frei zwischen den Clustern verschoben werden. Durch Anwendung des Hauptalgorithmus kann geprüft werden, ob die Verschiebung eines Subclusters in ein anderes Cluster zu einer Minimierung der Map Equation gegenüber der zuvor optimalen Clusterverteilung führt (Rosvall 2009).

Einzelobjekt-Verschiebung: Jedes Objekt wird erneut als separates Cluster betrachtet, sodass eine Verschiebung einzelner Objekte zwischen den im vorherigen Schritt bestimmten optimalen Clustern möglich ist. Durch Anwendung des Hauptalgorithmus kann festgestellt werden, ob die Verschiebung einzelner Objekte zwischen den Clustern zu einer weiteren Optimierung der Map Equation führen kann (Rosvall 2009). Die beiden Erweiterungen werden sequentiell wiederholt, bis die Map Equation nicht weiter minimiert werden kann und ein Optimum erreicht ist.

Wie funktioniert der Louvain-Algorithmus in einem einfachen Beispiel?

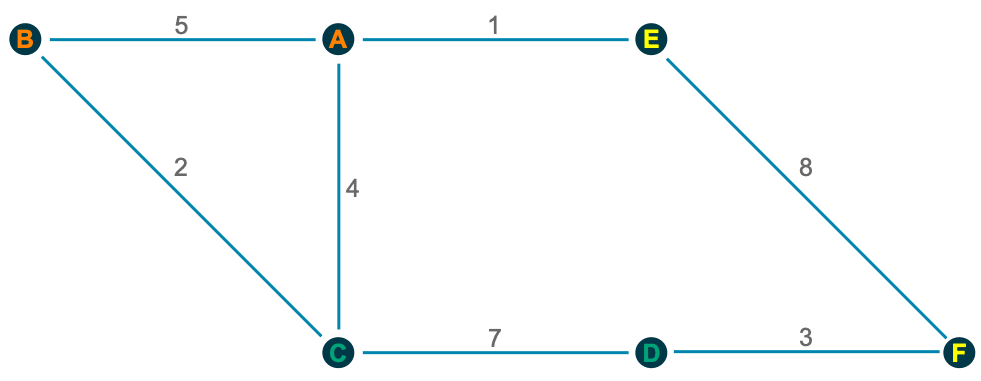
Wie wir sehen, besteht der Kern beider Methoden darin, Cluster zu bilden und Objekte in zwei Phasen neu zuzuweisen, um eine Zielfunktion zu optimieren. Um ein besseres Verständnis dafür zu bekommen, wie diese beiden Phasen funktionieren, möchte ich die Louvain Community Detection Methode anhand eines einfachen Beispiels veranschaulichen, eines Netzwerks mit sechs Knoten:

1. Phase

Zu Beginn wird jedes Objekt in einen eigenen Cluster eingeteilt, und wir müssen prüfen, ob die Modularität maximiert wird, wenn wir es einem anderen Cluster zuordnen. Nur eine positive Veränderung der Modularität führt zu einer Verschiebung des Clusters.

Für das Objekt A zum Beispiel sehen die Berechnungen wie folgt aus:

A → B: $ Q_{AB}=5-frac{10*7}{30}=2.667 $

A → C: $ Q_{AC}=4-frac{10*13}{30}=-0.333 $

A → E: $ Q_{AE}=1-frac{10*9}{30}=-2 $

In ähnlicher Weise können wir für alle anderen Objekte prüfen, ob eine Verschiebung in einen anderen Cluster die Modularität maximiert:

B → C: $Q_{BC}=2-frac{7*13}{30}=-1.033$

C → D: $Q_{CD}=7-frac{13*10}{30}=2.667$

D → F: $Q_{CD}=3-frac{10*11}{30}=-0.667$

E → F: $Q_{AB}=8-frac{9*11}{30}=4.7$

2. Phase

Nun versuchen wir, die in der 1. Phase gebildeten Cluster zu kombinieren:

Orange → Green: $ Q_{Or,Gr}=6-frac{7*9}{10}=-0.3 $

Orange → Yellow: $ Q_{Or, Ye}=1-frac{7*4}{10}=-1.8 $

Green → Yellow: $ Q_{Gr, Ye}=3-frac{9*4}{10}=-0.6 $

Wir können sehen, dass keine der Zuordnungen eines Clusters zu einem anderen Cluster die Modularität verbessern kann. Daher können wir Pass 1 beenden.

Da wir in der zweiten Phase des ersten Durchlaufs keine Veränderung haben, sind keine weiteren Durchläufe erforderlich, da bereits ein Maximum der Modularität erreicht ist. In größeren Netzwerken sind natürlich mehr Durchläufe erforderlich, da die Cluster dort aus deutlich mehr Objekten bestehen können.

In R wird nur das Paket igraph benötigt, um beide Methoden anzuwenden

Alles, was wir zur Anwendung dieser beiden Community Detection Algorithmen benötigen, ist das Paket igraph, das eine Sammlung von Netzwerk-Analysetools enthält, sowie zusätzlich eine Liste oder Matrix mit den Verbindungen zwischen den Objekten in unserem Netzwerk.

In unserem Beispiel verwenden wir das Les Misérables Characters Netzwerk, um die Charaktere in mehrere Gruppen zu clustern. Dazu laden wir den Datensatz lesmis, den man im Paket geomnet findet.

Wir müssen die Kanten aus lesmis extrahieren und in ein data.frame umwandeln. Anschließend muss dieses in einen igraph-Graphen konvertiert werden. Um die Gewichtungen jeder Verbindung zu nutzen, müssen wir die Spalte mit den Gewichten umbenennen, sodass der Algorithmus die Gewichtungen erkennen kann. Der resultierende Graph kann dann als Eingabe für die beiden Algorithmen verwendet werden.

# Libraries --------------------------------------------------------------

library(igraph)
library(geomnet)


# Data Preparation -------------------------------------------------------

#Load dataset
data(lesmis)

#Edges
edges <- as.data.frame(lesmis[1])
colnames(edges) <- c("from", "to", "weight")

#Create graph for the algorithms
g <- graph_from_data_frame(edges, directed = FALSE)

‍

Nun sind wir bereit, die Gemeinschaften mit den Funktionen cluster_louvain() bzw. cluster_infomap() zu finden

Außerdem können wir nachsehen, zu welcher Gemeinschaft die Zeichen gehören (membership()) oder eine Liste mit allen Gemeinschaften und deren Mitgliedern erhalten (communities()).

# Community Detection ----------------------------------------------------

# Louvain
lc <- cluster_louvain(g)
membership(lc)
communities(lc)
plot(lc, g)

# Infomap
imc <- cluster_infomap(g)
membership(imc)
communities(imc)
plot(lc, g)

‍

Wenn Sie diese Ergebnisse anschließend visualisieren möchten, schauen Sie sich meinen letzten Blogbeitrag an oder verwenden Sie die oben gezeigte plot()-Funktion zur schnellen Visualisierung. Wie Sie im Folgenden sehen können, ist die schnelle Plot-Option nicht so schön wie mit dem Paket visNetwork. Darüber hinaus ist sie auch nicht interaktiv.

Fazit

Beide Algorithmen übertreffen andere Community Detection Algorithmen (Lancchinetti, 2009). Sie zeigen eine ausgezeichnete Leistung, und Infomap liefert in dieser Studie leicht bessere Ergebnisse als Louvain. Darüber hinaus sollten wir zwei zusätzliche Punkte berücksichtigen, wenn wir zwischen diesen beiden Algorithmen wählen.

Erstens erledigen beide Algorithmen ihre Aufgabe sehr schnell. Wenn wir sie auf große Netzwerke anwenden, sehen wir, dass Louvain deutlich besser abschneidet.

Zweitens kann Louvain keine Ausreißer trennen. Dies könnte erklären, warum die Algorithmen Menschen in fast identische Cluster aufteilen, Infomap jedoch einige Personen aus bestimmten Clustern ausschließt, und diese dann ein eigenes Cluster bilden. Diese Punkte sollten wir im Hinterkopf behalten, wenn wir uns zwischen den beiden Algorithmen entscheiden müssen. Ein weiterer Ansatz könnte sein, beide zu verwenden und ihre Lösungen zu vergleichen.

Habe ich dein Interesse geweckt, deine eigenen Netzwerke zu clustern? Nutze gerne meinen Code oder kontaktiere mich, wenn du Fragen hast.

Literatur

• Blondel, Vincent D. / Guillaume, Jean L. / Lambiotte, Renaud / Lefebvre, Etienne (2008), “Fast unfolding of communities in large networks”, Journal of Statistical Mechanics: Theory and Experiment, Jg.2008, Nr.10, P10008
• Bohlin, Ludvig / Edler, Daniel / Lancichinetti, Andrea / Rosvall, Martin (2014), “Community Detection and Visualization of Networks with the Map Equation Framework”, in: Measuring Scholary Impact: Methods and Practice (Ding, Ying / Rousseau, Ronald / Wolfram, Dietmar, Eds.), S.3-34, Springer-Verlag, Berlin
• Lancichinetti, Andrea / Fortunato, Santo (2009), ” Community detection algorithms: a comparative analysis”, Physical review E, Jg.80, Nr.5, 056117
• Rosvall, Martin / Bergstrom, Carl T. (2008), “Maps of random walks on complexe net- works reveal community structure”, Proceedings of the National Academy of Sciences USA, Jg.105, Nr.4, S.1118-1123
• Rosvall, Martin / Axellson, Daniel / Bergstrom, Carl T. (2009), “The map equation”, The European Physical Journal Special Topics, Jg.178, Nr.1, S.13-23