Methoden Einführung: Statistik mit Löwen – Teil 2


Nach der deskriptiven Betrachtung der historischen Daten gehen unsere Archäologen einen Schritt weiter und stellen sich folgende Forschungsfrage:
H1: Je länger die Löwen bei den Zirkusspielen im Einsatz sind, desto höher ist ihr Gewicht.
Für die Beantwortung dieser Frage bedienen sich die Forscher zunächst einer einfachen Korrelationsanalyse.
pwcorr gewicht monate, sig obs
Diese fördert zu Tage, dass das Gewicht und die Monate im Zirkus positiv mit Pearson’s Rho $rho$ = .7718 und einer Signifikanz von p $le$.001 korrelieren. Die Löwen wurden also schwerer, je länger sie sich im Zirkus befanden.
Jedoch wussten die auswertenden Statistiker aus der vorherigen Analyse, dass die Gewichtszunahme nicht kontinuierlich fortschritt. Vor allem bei Löwen, die schon länger im Zirkus waren, konnte man graphisch erkennen, dass hier das Gewicht wieder abnahm. Daher kategorisierten die Wissenschaftler die Monate, um mit der neuen Variable eine Varianzanalyse (ANOVA) durchführen zu können.
tab monate_kat
Ziel der ANOVA ist es nun sich anzusehen, ob das durchschnittliche Gewicht zwischen den neu gebildeten Gruppen verschieden ist, und (Vorteil ANOVA gegenüber einer Korrelation) in welche Richtung sich das Gewicht unterscheidet. Dabei stellt das Verfahren mehrere Anforderungen an die Daten, die in Teil 2 dieser Reihe einzeln betrachtet werden sollen.
Voraussetzungen einer ANOVA
Annahme 1: Die abhängige Variable (Gewicht) sollte metrisch sein. Gewicht entspricht aufgrund des Nullpunkts einer Verhältnisskala (Ratioskala).
Annahme 2: Die unabhängige Variable (Monate in Kategorien) sollte aus mindestens 3 Kategorien bestehen. Unsere Variable besteht aus insgesamt 6 Kategorien und scheint somit bestens geeignet.
Annahme 3: Es sollten unabhängige Beobachtungen vorliegen. Dies bedeutet, dass zwischen den Beobachtungen in und zwischen jeder Gruppe kein Zusammenhang bestehen sollte.
Während die ersten drei Annahmen nicht mit einem statistischen Verfahren überprüft werden können, ist die bei den nunmehr folgenden Annahmen der Fall.
Annahme 4: Es sollten keine signifikanten Ausreißer existieren. Die Überprüfung dieser Annahme erfolgt graphisch mit Hilfe von Boxplots. Wie man hier untenstehend erkennen kann, liegen statistisch gesehen keine vor, da ansonsten in der Darstellung Punkte ober- bzw. unterhalb der Antennen vorhanden wären.
graph box gewicht, over(monate_kat, label(labsize(vsmall)))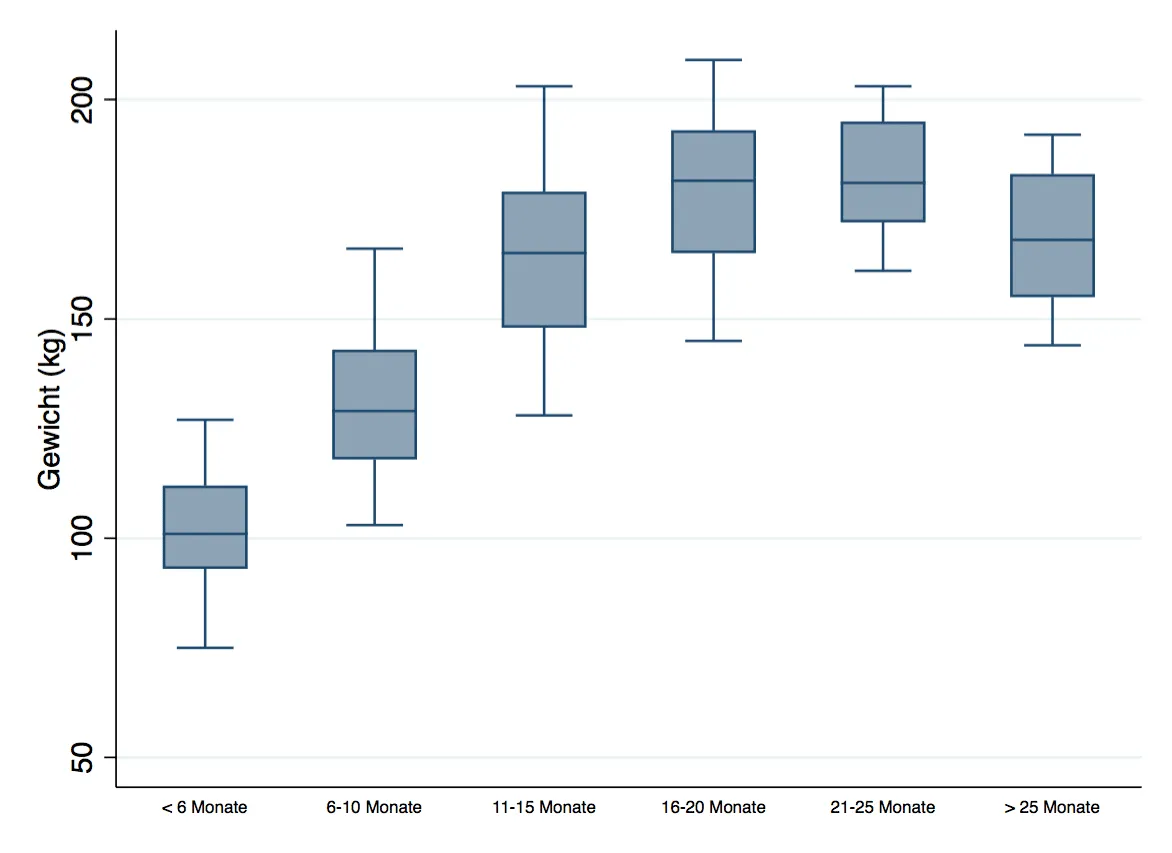
Statistisch gesehen ist die Berechnung von Ausreißern sehr einfach: Ausgehend vom oberen und unteren Ende der Box (75% bzw. 25% Quartil) wird der Interquartilsabstand (für jede Gruppe) berechnet.
Formel: $IQR = x_{0.75} – x_{0.25}$
Für die Löwen, die weniger als 6 Monate im Zirkus sind, kann dies mit dem Stata command
centile gewicht if monate_kat == 1, centile(25 75)
berechnet werden. So ist der 75% Quartil in dieser Gruppe 112kg und das 25% Quartil 93kg. Der IQR somit 112kg - 93kg = 19kg.
Ein Ausreißer „nach oben“ bzw. „nach unten“ ist so definiert, dass das 1.5-fache der Kantenlänge nicht überschritten werden darf. Dies gilt als Standardwert in der Berechnung von Ausreißern, so dass das Ende der Antennen beim Boxplot exakt diesen Schwellenwert darstellt. Berechnet wird dies mit
$Ausreißer_{oben} = |{frac{ Wert - Quartil_{0,75} }{ IQR } }|Ausreißer_{unten} = |{frac{ Wert - Quartil_{0,25} }{ IQR } }| $
Am Beispiel der Löwen in Kategorie 1 (weniger als 6 Monate im Zirkus) lassen wir uns das minimale und maximale Gewicht anzeigen.
su gewicht if monate_kat == 1
Das minimale Gewicht dieser Löwen beträgt 75kg, das Maximalgewicht 127kg. Der Anteil am IQR ist damit:
$Ausreißer_{oben} = |{frac{ 127 - 112 }{ 19 } }| = 0.789 le 1.5 Ausreißer_{unten} = |{frac{ 75 - 93 }{ 19 } }| = 0.947 le 1.5 $
Da also das Minimum und Maximum in dieser Gruppe den Wert 1.5 nicht überschreitet, liegen keine Ausreißer vor. Stata liefert von Haus aus leider keine Berechnung inklusive Anzeige von Ausreißern nach dieser Logik mit, jedoch lässt sich der Befehl „extremes“ zusätzlich installieren. Der Befehl führt die eben besprochenen Berechnungen sofort durch und würde Ausreißerwerte anzeigen.
ssc install extremes
bysort monate_kat: extremes gewicht, iqr(1.5)
Da die Eingabe des Befehls, gruppiert nach den Kategorien der Monate, keine Werte zeigt, bestätigt sich die graphische Betrachtung der Boxplots natürlich.
Annahme 5: Die abhängige Variable (Gewicht) sollte innerhalb jeder Kategorie (Monate) normalverteilt sein. Normalverteilung wird aus unserer Erfahrung oftmals als casus belli für den weiteren Verlauf der Analyse betrachtet. Nahezu stoisch wird dafür gern ausschließlich der eher nicht zu empfehlende Kolmogorov-Smirnov-Test (Field 184 ff.) verwendet, ohne sich dabei auch die graphische Verteilung selbst anzusehen. Die unten stehenden Histogramme betrachten die Verteilung des Gewichts über alle 6 Kategorien der Monate hinweg und geben zudem das Ergebnis des empfohlenen Shapiro-Wilk-Tests auf Normalverteilung wieder. Ist bei diesem Test (ähnlich wie Kolmogorov-Smirnov) die Signifikanz p $le$.05, so kann die Variable als normalverteilt gelten.

Für drei der sechs Kategorien gilt per Test mit p $le$.05, dass keine Normalverteilung vorliegt. Optisch jedoch lässt sich auch bei diesen 3 Kategorien keine grobe Verletzung feststellen, so dass auch hier kein Einwand gegen die Auswertung mit der ANOVA besteht. Zudem sei auf die zahlreiche Literatur hinsichtlich der Robustheit der ANOVA bei Verletzung dieser Voraussetzung verwiesen.
Annahme 6: Die letzte Annahme der ANOVA ist, dass die Varianzen zwischen den Gruppen hinsichtlich der abhängigen Variable gleich sind. Dies bezeichnet man auch als Homogenität der Varianzen. Mit alleinigem Blick auf die Varianz kann man dies nur schwer beurteilen (siehe untere Tabelle), so dass ein Test auf Varianzhomogenität durchgeführt werden muss.
tabstat gewicht, statistics(mean var) by(monate_kat)
Dieser Test ist der Levene-Test, der mit p $ge$ .05 Varianzhomogenität nachweist und in Stata über
robvar gewicht, by(monate_kat)
anzufordern ist. Die Ausgabe des Levene-Tests ist in Stata mit W0 gekennzeichnet und zeigt in diesem Fall p $le$.001 an, so dass nicht von der Homogenität der Varianzen gesprochen werden kann. In diesem Fall sollte für die Berechnung der F-Werte der ANOVA eine Korrektur per Welch oder Brown-Forsythe durchgeführt werden, ebenso existieren posthoc-Tests für die Verletzung dieser Annahme. Im Gegensatz zu SPSS verfügt Stata nicht über eine Option innerhalb des Befehls, um Welch oder Brown-Forsythe anzuwenden, jedoch sei auch hier auf die Robustheit der ANOVA hingewiesen. Zudem verfügt Stata mit Hilfe des Regressionsbefehls, welcher komplementär zur ANOVA verwendet werden kann, über weitaus größere Möglichkeiten der Berechnung beim Auftreten dieses Problems. Für unsere Analysten stellt daher die Verletzung der Varianzhomogenität im Moment kein Problem dar.
Auf ein Wort
Die Annahmen der ANOVA werden gern als heilig und unumstößliches Gesetz betrachtet. Oftmals wird bereits bei Verletzung einer Annahme, auf die die ANOVA durchaus robust reagiert, ein nicht-parametrisches Alternativverfahren verwendet. Mehr noch, nicht selten werden Mittelwerte über die Gruppen deskriptiv dargestellt und dann mit den Ergebnissen (Signifikanzen) des nicht-parametrischen Verfahrens interpretiert. Insgesamt ist die ANOVA ein robustes Verfahren, welches sich auch bei groben Verletzungen der Annahmen noch anwenden lässt.
Referenzen
- Field, Andy (2013): Discovering Statistics Using SPSS, 4th Edition. SAGE: London


