Einführung in Reinforcement Learning – wenn Maschinen wie Menschen lernen


Die meisten Machine Learning Algorithmen, die heute in der Praxis Anwendung finden, gehören zur Klasse des überwachten Lernens (Supervised Learning). Im Supervised Learning wird dem Machine Learning Modell ex post eine bereits bekannte Zielgröße $y$ präsentiert, die auf Basis verschiedener Einflussfaktoren $X$ in den Daten durch eine Funktion $f$ möglichst genau vorhergesagt werden soll. Die Funktion $f$ repräsentiert dabei abstrakt das jeweilige Machine Learning Modell, das ein Mapping zwischen den Inputs und den Outputs des Modells bereitstellt.
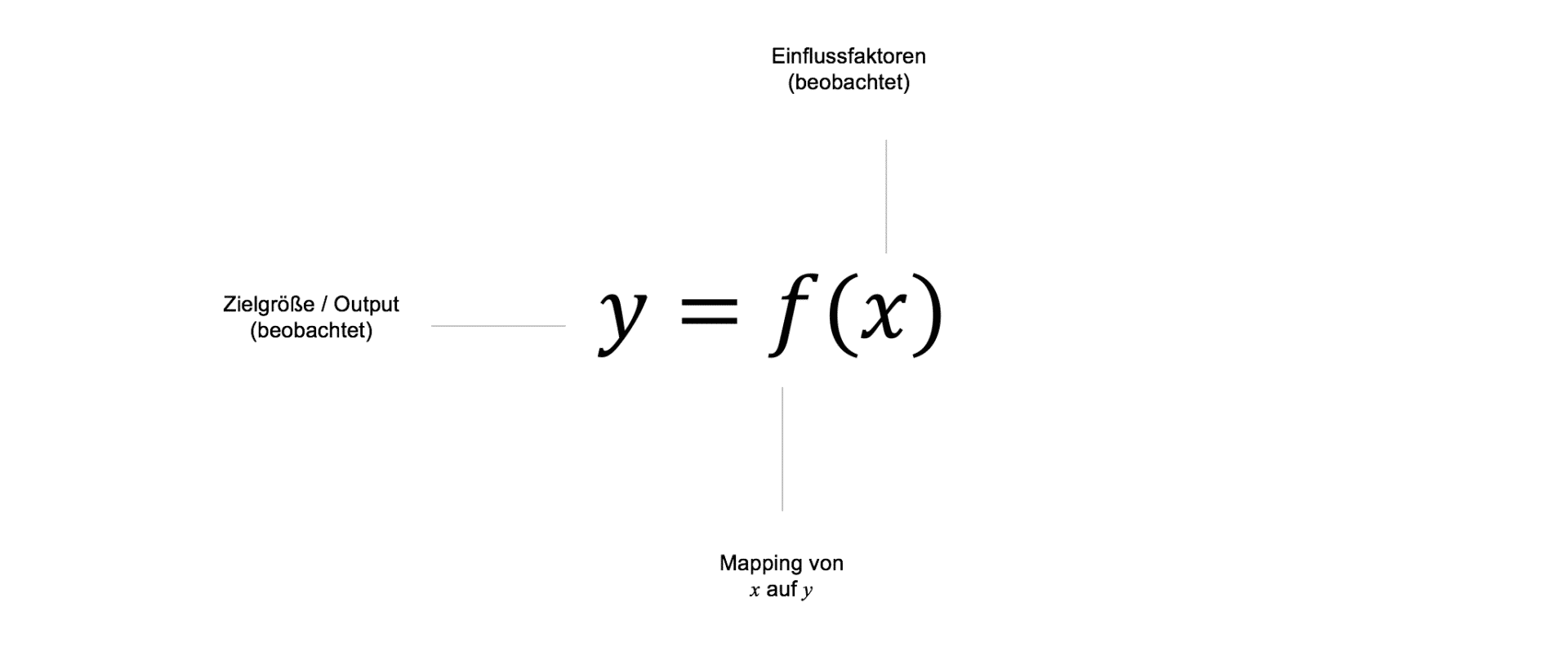
Die gelernten Zielgrößen einfacher ML Modelle sind somit i.d.R. statisch und verändern sich nur im historischen Zeitverlauf, der ex post bereits bekannt ist. Im Zeitverlauf können neue Datenpunkte gesammelt werden, diese fließen dann in Form eines "Retrainings" in das gelernte Mapping $f$ zwischen $X$ und $y$ ein.
Basierend auf den Prognosen eines Modells werden im Anschluss weitere, meist noch menschlich gesteuerte, Handlungen ausgelöst. Diese stellen oft die eigentlichen Entscheidungen dar, die geschäftsrelevante Auswirkungen bzw. Implikationen nach sich ziehen. Die eigentlichen Geschäftsentscheidungen, die auf Basis von ML Modellen getroffen werden, sind somit vielerorts noch nicht bzw. nur teilweise maschinengesteuert. Nur an sehr wenigen Stellen werden heute bereits vollständig autonom agierende Modelle angewendet, die in der Lage sind, autark Entscheidungen zu treffen und ihr Handeln zu überwachen bzw. modellbasiert anzupassen.
Auf dem Weg hin zu selbstlernenden, autonomen Algorithmen, wie sie im Bereich der künstilichen Intelligenz verwendet werden müssen, liefern Modelle aus dem supervised learning somit nur einen begrenzten Beitrag.
Auf dem Weg hin zu selbstlernenden, autonomen Algorithmen, wie sie im Bereich der künstlichen Intelligenz verwendet werden müssen, liefern Modelle aus dem Supervised Learning somit nur einen begrenzten Beitrag. Dies ist meist darin begründet, dass die von Machine Learning Modellen gelernte 1:1 Beziehung zwischen Inputs und Outputs in komplexeren Szenarien oder Handlungsumgebungen nicht mehr ausreichend ist. Beispielweise sind die meisten Machine Learning Modelle damit überfordert, mehrere Zielgrößen gleichzeitig oder eine Sequenz von Zielgrößen bzw. Handlungen zu erlernen. Weiterhin kann der Zusammenhang zwischen Einflussfaktoren und Zielgrößen in Abhängigkeit der Umgebung bzw. auf Basis bereits getroffenener Prognosen und Entscheidungen unmittelbar variieren, was ein fortlaufendes "Retraining" der Modelle unter geänderten Rahmenbedingungen implizieren würde.
Damit Machine Learning Modelle auch in Umgebungen Anwendung finden können, in denen sie eigenständige Aktions-Reaktions Ereignisse erlernen können, werden Lernverfahren benötigt, die einer sich verändernden Dynamik der Umgebung Rechnung tragen. Ein populäres Beispiel für die erfolgreiche Anwendung von Algorithmen dieser Art ist der Sieg von Goolge's KI AlphaGo über den weltbesten menschlichen Go-Spieler. AlphaGo wäre mit klassischen Methoden des Supervised Learning nicht darstellbar gewesen, da aufgrund der unendlichen Anzahl an Spielzügen und Szenarien kein Modell in der Lage gewesen wäre, die Komplexität der Aktions-Reaktions-Beziehungen als reines Input-Output-Mapping abzubilden. Stattdessen werden Methoden benötigt, die in der Lage sind, selbständig auf neue Gegebenheiten der Umgebung zu reagieren, mögliche zukünftige Handlungen zu antizipieren und diese in aktuelle Entscheidung mit einfließen zu lassen. Die Klasse der Lernverfahren, auf denen Systeme wie AlphaGo basieren werden als Reinforcement Learning bezeichnet.
Was ist Reinforcement Learing?
Reinforcement Learning (RL) bildet neben Supervised und Unsupervised Learning die dritte große Gruppe von Machine Learning Verfahren. RL ist eine am natürlichen Lernverhalten des Menschen orientierte Methode. Menschliches Lernen erfolgt, insbesondere in frühen Stadien des Lernens, häufig über eine einfache Exploration der Umwelt. Dabei sind unsere Handlungen im Rahmen des Lernproblems durch einen gewissen Aktionsraum definiert. Über "Trial and Error" werden die Auswirkungen verschiedener Handlungen auf unsere Umwelt beobachtet und bewertet. Als Reaktion auf unsere Handlungen erhalten wir von unserer Umgebung ein Feedback, abstrakt dargestellt in Form einer Belohnung oder Bestrafung. Dabei ist das Konzept der Belohnung bzw. Bestrafung nur in den allerwenigsten Fällen monetär zu verstehen. In vielen Fällen wird die Belohnung in Form von sozialer Akzeptanz, Lob anderer Menschen aber auch durch persönliches Wohlbefinden oder Erfolgserlebnisse ausgezahlt. Vielfach zeigt sich auch eine zeitliche Latenz zwischen Handlung und Belohnung. Hierbei versucht der Mensch häufig, durch sein Handeln die erwartete "Gesamtbelohnung" im Zeitverlauf zu maximieren und nicht nur unmittelbare Belohnungen zu generieren.
Ein Beispiel: Wenn wir lernen Gitarre zu spielen, umfasst unser Aktionsraum das Zupfen der Seiten sowie das Greifen am Bund. Über eine zunächst zufällige Exploration des Handlungsraums erhalten wir in Form von Tönen der Gitarre ein Feedback der Umwelt. Dabei werden wir belohnt, wenn die Töne "gerade" sind bzw. bestraft, wenn die Nachbarn mit dem Besen von unten gegen die Decke klopfen. Wir versuchen, die erwartete Gesamtbelohnung in Form von richtig gespielten Noten und Akkorden im für uns relevanten Zeithorizont zu maximieren. Dies geschieht nicht dadurch, dass wir aufhören zu lernen sobald wir einen Akkord sauber spielen können, sondern manifestiert sich durch ein stetiges Training und immer wieder neue Belohnungen und Erfolge, die uns im Zeitverlauf erwarten. Natürlich kann die Dauer der Exploration der möglichen Handlungen und Belohnungen der Umwelt durch die Hinzunahme eines externen Trainers verbessert werden. Dieses Beispiel ist natürlich sehr vereinfacht, stellt aber das Grundprinzip im Kern gut dar.
Reinforcement Learning besteht formal betrachtet aus fünf wichtigen Komponenten, nämlich (1) dem Agenten (agent), (2) der Umgebung (environment), (3) dem Status (state), (4) der Aktion (action) sowie (5) der Belohnung (reward). Grundsätzlich lässt sich der Ablauf wie folgt beschreiben: Der Agent führt in einer Umgebung zu einem bestimmten Status ($s_t$) eine Aktion ($a_t$) aus dem zur Verfügung stehenden Aktionsraum $A$ durch, die zu einer Reaktion der Umgebung in Form einer Belohnungen ($r_{t}$) führt.
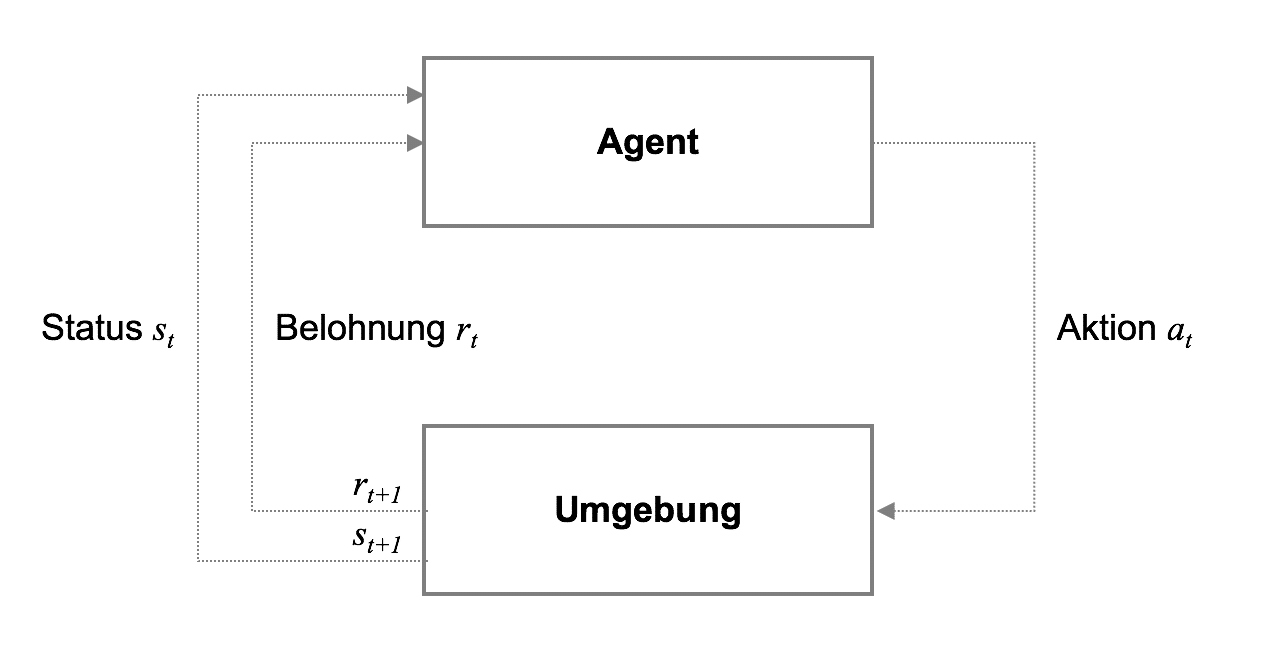
Die Reaktion der Umgebung auf die Aktion des Agenten beeinflusst nun wiederum die Wahl der Aktion des Agenten im nächsten Status ($s_{t+1}$). Über mehrere tausend, hunderttausend oder sogar millionen von Iterationen ist der Agent in der Lage, einen Zusammenhang zwischen seinen Aktionen und dem künftig zu erwartenden Nutzen in jedem Status zu approximieren und sich somit entsprechend optimal zu verhalten. Dabei befindet sich der Agent immer in einem Dilemma zwischen der Nutzung seiner bisher erworbenen Erfahrung auf der einen und der Exploration neuer Strategien zur Erhöhung der Belohnung auf der anderen Seite. Dies wird als "Exploration-Exploitation Dilemma" bezeichnet.
Die Approximation des Nutzens kann dabei modellfrei, also über reine Exploration der Umgebung erfolgen oder durch die Anwendung von Machine Learning Modellen, die den Nutzen einer Aktion versuchen zu approximieren. Letztere Variante wird insbesondere dann angewendet, wenn der Status- und/oder Aktionsraum von hoher Dimensionalität ist.
Q-Learning
Um Reinforcement Learning Systeme zu trainieren, wird häufig eine Methode verwendet, die als Q-Learning bekannt ist. Den Namen erhält Q-Learning von der sog. Q-Funktion $Q(s,a)$, die den erwarteten Nutzen $Q$ einer Aktion $a$ im Status $s$ beschreibt. Die Nutzenwerte werden in der sog. Q-Matrix $Q$ gespeichert, deren Dimensionalität sich über die Anzahl der möglichen Stati sowie Aktionen definiert. Während des Trainings versucht der Agent, die Q-Werte der Q-Matrix durch Exploration zu approximieren, um diese später als Entscheidungsregel zu nutzen. Die Belohnungsmatrix $R$ enthält, korrespondierend zu $Q$, die entsprechenden Belohnungen, die der Agent in jedem Status-Aktions-Paar erhält.
Die Approximation der Q-Werte funktioniert im einfachsten Falle wie folgt: Der Agent startet in einem zufällig initialisierten Status $s_t$. Anschließend selektiert der Agent zufällig eine Aktion $a_t$ aus $A$, beobachtet die entsprechende Belohnung $r_t$ und den darauf folgenden Status $s_{t+1}$. Die Update-Regel der Q-Matrix ist dabei wie folgt definiert:
$$Q(s_t,a_t)=(1-\alpha)Q(s_t, a_t)+\alpha(r_t+\gamma \max Q(s_{t+1},a))$$
Der Q-Wert im Status $s_t$ bei Ausführung der Aktion $a_t$ ist eine Funktion des bereits gelernten Q-Wertes (erster Teil der Gleichung) sowie der Belohnung im aktuellen Status zzgl. des diskontierten maximalen Q-Wertes aller möglichen Aktionen $a$ im folgenden Status $s_{t+1}$.
Der Parameter $\alpha$ im ersten Teil der Gleichung wird als Lernrate (learning rate) bezeichnet und steuert, zu welchem Anteil eine neu beobachtete Information den Agenten in seiner Entscheidung eine bestimmte Aktion zu treffen beeinflusst.
Der Parameter $\gamma$ ist der sog. Diskontierungsfaktor (discount factor) und steuert den Trade-off zwischen der Präferenz von kurzfristigen oder zukünftigen Belohnungen in der Entscheidungsfindung des Agenten. Kleine Werte für $\gamma$ lassen den Agenten eher Entscheidungen treffen, die näher liegende Belohnungen in der Entscheidungsfindung priorisieren, während höhere Werte für $\gamma$ den Agenten langfristige Belohnungen in der Entscheidungsfindung priorisieren lassen.
In modellbasierten Q-Learning Umgebungen findet die Exploration der Umgebung nicht rein zufällig statt. Die Q-Werte der Q-Matrix werden basierend auf dem aktuellen Status durch Machine Learning Modelle, in der Regel neuronale Netze und Deep Learning Modelle, approximiert. Häufig wird während des Trainings von modellbasierten RL Systemen noch eine zufällige Handlungskomponente implementiert, die der Agent mit einer gewissen Wahrscheinlichkeit $p \lt \epsilon$ durchführt. Dieses Vorgehen wird als $\epsilon$-greedy bezeichnet und soll verhindern, dass der Agent immer nur die gleichen Aktionen bei der Exploration der Umgebung durchführt.
Nach Abschluss der Lernphase wählt der Agent in jedem Status diejenige Aktion mit dem höchsten Q-Wert aus, $\max Q(s_t, a)$. Somit kann sich der Agent von Status zu Status bewegen und immer diejenige Aktion wählen, die den approximierten Nutzen maximiert.
Q-Learning eignet sich insbesondere dann als Lernverfahren, wenn die Anzahl der möglichen Stati und Aktionen überschaubar ist. Andernfalls wird das Problem aufgrund der kombinatorischen Komplexität mit reinen Explorationsmechanismen nur schwer lösbar. Aus diesem Grund findet in extrem hochdimensionalen Status- und Aktionsräumen die Approximation der Q-Werte häufig über modellbasierte Ansätze statt.
Eine weitere Schwierigkeit bei der Anwendung von Q-Learning zeigt sich, wenn die Belohnungen zeitlich sehr weit vom aktuellen Status- und Handlungsraum des Agenten entfernt liegen. Wenn in naheliegenden Stati keine Belohnungen vorhanden sind, kann der Agent erst nach einer lagen Explorationsphase weit in der Zukunft liegende Belohnungen in die naheliegenden Stati propagieren.
Minimalbeispiel für Q Learning
Der neue, autonome Stabsaugerroboter "Dusty3000" der Firma STAUBWORX soll sich vollautomatisch in unbekannten Wohnungen zurecht finden. Dabei nutzt das Gerät einen Reinforcement Learning Ansatz, um herauszufinden, in welchen Räumen einer Wohnung sich Staubballen und Flusen anhäufen. Eine virtuelle Testwohnung, in der der Roboter kalibriert werden soll, hat den folgenden Grundriss:
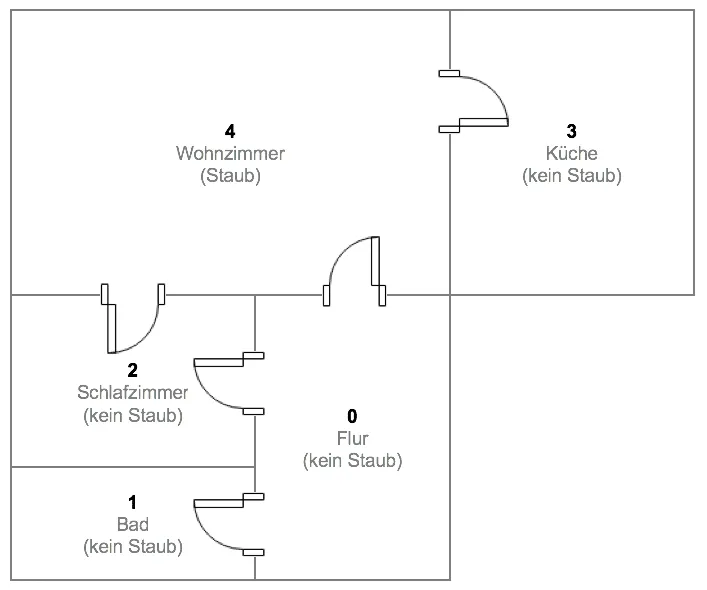
Insgesamt verfügt die virtuelle Testwohnung über 5 Zimmer, wobei im Testszenario lediglich im Wohnzimmer Staub anzufinden ist. Findet der Roboter den Weg zum Staub, erhält er eine Belohnung von $r = 1$ andernfalls wird keine Belohnung angesetzt $r=0$. Räume, die der Roboter von seiner aktuellen Position aus nicht erreichen kann, werden in der Belohnungsmatrix mit $r=-1$ definiert. In Matrizenschreibweise stellen sich die Belohnungen sowie die möglichen Aktionen pro Raum wie folgt dar:
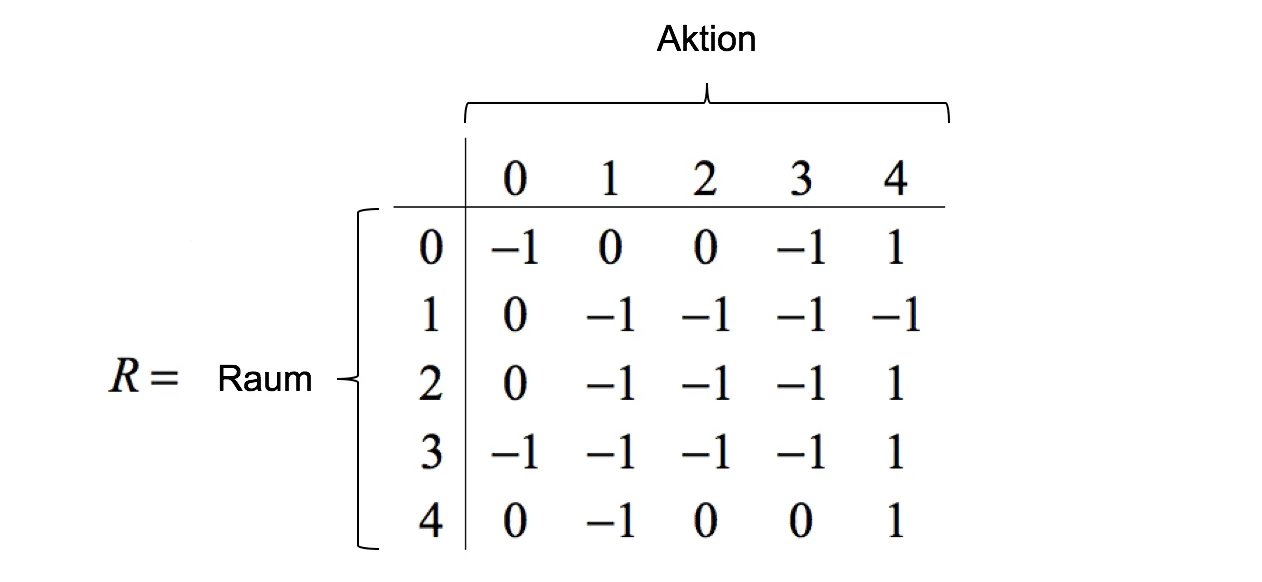
Stellen wir uns vor, der Saugroboter startet seine Erkundung zufällig im Flur (Raum 0). Ausgehend vom aktuellen Raum (Status) $s=0$ bieten sich dem Roboter drei mögliche Aktionen: 1, 2 oder 4. Aktion 0 und 3 sind nicht möglich, da diese Räume vom Flur aus nicht erreichbar sind. Der Agent erhält keine Belohnung, wenn er Aktion $a=1$ wählt und sich vom Flur in Raum 1 (Bad) begibt. Das gleiche gilt für Aktion $a=2$ (Bewegung ins Schlafzimmer). Wählt der Roboter jedoch Aktion $a=4$ und fährt ins Wohnzimmer, so findet er dort den Staub und er erhält eine Belohnung von $r=1$. Für den externen Betrachter erscheint die Wahl der Aktion trivial, unser Roboter jedoch kennt seine Umgebung nicht und wählt zufällig aus den zur Verfügung stehenden Aktionen aus.
Der Roboter startet die zufällige Erkundung der Wohnung. Die Lernrate wird auf $\alpha=1$ und der Diskontierungsfaktor auf $\gamma=0.95$ gesetzt. Basierend auf dem Startpunkt im Flur wählt er per Zufallsgenerator aus den zur Verfügung stehenden Aktionen $a=2$ aus. Somit initiiert der Roboter zunächst eine Bewegung ins Schlafzimmer. Im vereinfachten Fall von $\alpha=1.0$ is der Q Value für die Bewegung vom Flur ins Schlafzimmer ist definiert durch:
$$Q(0,2)=(1-\alpha)Q(0,2)+\alpha(r_t+\gamma \max Q(s_{t+1},a))$$$$=(1-1)*0+1*(0+0.95\max[Q(2,0),Q(2,4)])$$$$=0+1*(0+0.95 \max[0, 1])=0.95$$
Hier zeigt sich auch die Bedeutung des Diskontierungsfaktors: Bei einem Wert von 0 würde die mögliche Bewegung vom Schlafzimmer aus ins Wohnzimmer bei der momentanen Bewegung vom Flur ins Schlafzimmer nicht berücksichtigt werden. Es ergäbe sich Q Value von $Q(0,2)=0$. Da der Diskontierungsfaktor in unserem Beispiel aber größer 0 ist, wird auch die mögliche, zukünftige Belohnung in $Q(0,2)$ mit eingepreist.
Im Schlafzimmer angekommen ergeben sich wiederum zwei mögliche Aktionen. Entweder der Roboter bewegt sich zurück in den Flur, $a=0$ oder er fährt weiter ins Wohnzimmer, $a=4$. Zufällig fällt die Wahl diesmal auf das Wohnzimmer, womit sich folgender Q Value ergibt
$$Q(2,4)=(1-\alpha)+\alpha(r_t+\gamma \max Q(s_{t+1},a)) $$$$=(1-1)*0+1*(1+0.95\max[Q(4,0),Q(4,3)]) $$$$ =0+1*(1+0.95\max[0,0])=1$$
Der gesamte Vorgang der Exploration bis hin zur Belohnung wird als eine Episode bezeichnet. Da der Roboter nun am Ziel angekommen ist, wird die Episode beendet. Während dieses Durchlaufs konnte der Agent zwei Q-Werte berechnen. Diese werden in die Q-Matrix eingetragen, die sozusagen das Gedächtnis des Roboters abbildet.
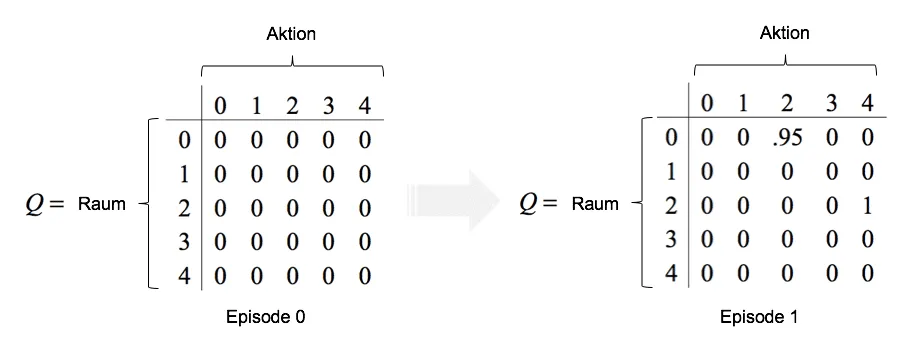
Im weiteren Trainingsverlauf werden nun Schritt für Schritt die Werte der Q-Matrix durch den Algorithmus aktualisiert. Der Roboter entscheidet sicht in jedem Raum für diejenige Aktion, die den höchsten Q-Wert aufweist. Die Exploration der Umgebung endet dann, wenn der Agent eine Belohnung erhalten hat.
Implementierung in Python
Zur Verdeutlichung des obigen Beispiels findet sich im Folgenden der Programmiercode zur Umsetzung in Python. Zunächst wird eine Funktion erstellt, die in Abhängigkeit der Belohnungsmatrix R der Lernrate alpha, dem Diskontierungsfaktor gamma sowie der Episodenzahl episodes den oben skizzierten Algorithmus durchführt.
# Imports
import numpy as np
# Funktion
def q_learning(R, gamma, alpha, episodes):
""" Funktion für Q Learning """
# Anzahl der Zeilen und Spalten der R-Matrix
n, p = R.shape
# Erstellung der Q Matrix (0-Werte)
Q = np.zeros(shape=[n, p])
# Loop Episoden
for i in range(episodes):
# Zufälliger Startpunkt des Roboters
state = np.random.randint(0, n, 1)
# Iteration
for j in range(100):
# Mögliche Rewards im aktuellen Status
rewards = R[state]
# Mögliche Bewegungen des Roboters im aktuellen Status
possible_moves = np.where(rewards[0] > -1)[0]
# Zufällige Bewegung des Roboters
next_state = np.random.choice(possible_moves, 1)
# Update der Q values berechnen
Q[state, next_state] = (1 - alpha) * Q[state, next_state] + alpha * (
R[state, next_state] + gamma * np.max(Q[next_state, :]))
# Abbrechen der Episode wenn Ziel erreicht
if R[state, next_state] == 1:
break
# Q-Matrix zurückgeben
return Q
Zunächst wird die Anzahl der Stati n sowie die Anzahl der Aktionen p bestimmt. Diese werden aus der Belohnungsmatrix R abgeleitet. Anschließend wird die zunächst noch leere Matrix Q erstellt, die die Q-Werte während der Lernphase speichert. In der Schleife über die Anzahl der festgelegten Episoden episodes wird zunächst ein zufälliger Startpunkt für den Agenten gewählt. Anschließend wird in j=100 Iterationen der oben beschriebene Algorithmus durchgeführt: Aus der Menge möglicher Aktionen possible_moves für den aktuellen Status state wird eine zufällige Auswahl getroffen und in der Variable next_state gespeichert. Im Anschluss daran findet das Update der Q-Werte, gem. oben beschriebener Formel statt. Hierbei werden sowohl der aktuelle Q-Wert an der Stelle Q[state, next_state] als auch die Belohnung des aktuellen Status R[state, next_state] verarbeitet. Nach der Aktualisierung der Q-Werte wird noch geprüft, ob der Agent die Belohnung erhalten hat. Falls ja, wird der innere Loop beendet und die Simulation geht in die nächste Episode. Nach Beendigung aller Episoden wird die finale Q-Matrix zurückgegeben.
Eine praktische Anwendung der oben gezeigten Funktion findet sich in der unten stehenden Codebox. Zunächst wird die Belohnungsmatrix analog für das oben skizzierte Beispiel definiert, die dann mit den weiteren Funktionsargumenten an die Funktion q_learning übergeben wird. Die Lernrate wird auf $\alpha=0.8$ und der Diskontierungsfaktor auf $\gamma=0.95$ gesetzt. Insgesamt sollen $n=1000$ Episoden simuliert werden.
# Anzahl der Räume
rooms = 5
# Belohnungs-Matrix
R = np.zeros(shape=[rooms, rooms])
R[0, :] = [-1, 0, 0, -1, 1]
R[1, :] = [ 0, -1, -1, -1, -1]
R[2, :] = [ 0, -1, -1, -1, 1]
R[3, :] = [-1, -1, -1, -1, 1]
R[4, :] = [ 0, -1, 0, 0, 1]
# Q-Learning
Q = q_learning(R=R, gamma=0.95, alpha=0.8, episodes=1000)
# Finale Q Matrix normalisieren und anzeigen
np.round(Q / np.max(Q), 4)
array([[ 0. , 0.9025, 0.95 , 0. , 1. ],
[ 0.95 , 0. , 0. , 0. , 0. ],
[ 0.95 , 0. , 0. , 0. , 1. ],
[ 0. , 0. , 0. , 0. , 1. ],
[ 0.95 , 0. , 0.95 , 0.95 , 1. ]])
An der finalen Q-Matrix kann man nun die gelernten Handlungen des Roboters ablesen. Dies geschieht durch Ablesen des maximalen Q-Wertes pro Status (Zeile). Beispiel: Befindet sich der Roboter im Flur (Zeile 1 der Matrix) so ist der maximale Q-Wert in der letzten Spalte zu finden. Dies korrespondiert zu einer Bewegung ins Wohnzimmer. Befindet sich der Agent im Bad (Zeile 2) bewegt er sich zunächst in den Flur (Zeile 1). Von dort bestimmt der maximale Q-Wert eine Bewegung ins Wohnzimmer.
Ein komplexeres Beispiel
Unser Dusty3000 hat sich in der einfachen Simulationsumgebung bereits bewährt. Nun soll geklärt werden, wie sich der Roboter in komplexeren Wohnungen zurecht finden kann. Zu diesem Zweck wurde die Wohnung um zwei weitere Zimmer ergänzt und der Staub vom Wohnzimmer ins Kinderzimmer verlegt:
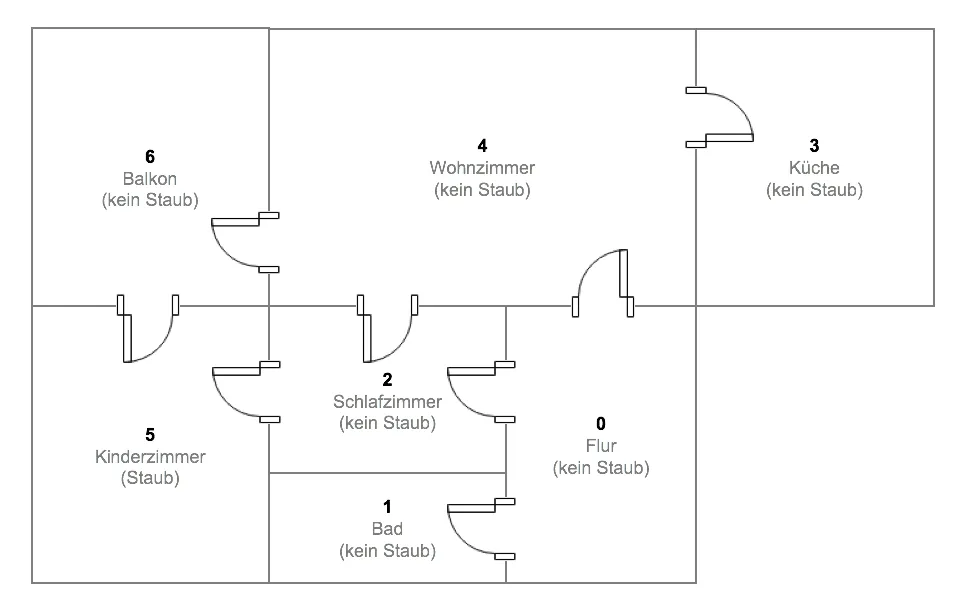
Das Kinderzimmer ist im Vergleich zum vorherigen Beispiel deutlich schwieriger und nur über verschiedene Pfade zu erreichen. Somit wird der Roboter es schwerer haben, die Q-Werte richtig zu schätzen. Die Belohnungsmatrix verändert sich entsprechend wie folgt:
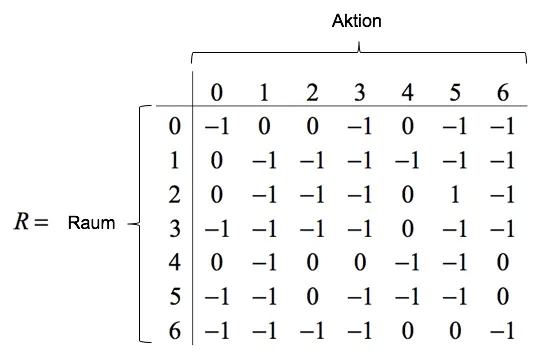
Analgog zum vorhergehenden Beispiel wird die Lernrate auf $\alpha=0.8$ und der Diskontierungsfaktor auf $\gamma=0.95$ gesetzt. Insgesamt werden $n=1000$ Episoden simuliert.
# Anzahl der Räume
rooms = 7
# Belohnungs-Matrix
R = np.zeros(shape=[rooms, rooms])
R[0, :] = [-1, 0, 0, -1, 0, -1, -1]
R[1, :] = [ 0, -1, -1, -1, -1, -1, -1]
R[2, :] = [ 0, -1, -1, -1, 0, 1, -1]
R[3, :] = [-1, -1, -1, -1, 0, -1, -1]
R[4, :] = [ 0, -1, 0, 0, -1, -1, 0]
R[5, :] = [-1, -1, 0, -1, -1, -1, 0]
R[6, :] = [-1, -1, -1, -1, 0, 0, -1]
# Q-Learning!
Q = q_learning(R=R, gamma=0.95, alpha=0.8, episodes=1000)
# Normalize
np.round(Q / np.max(Q), 4)
array([[ 0. , 0.8571, 0.9499, 0. , 0.9023, 0. , 0. ],
[ 0.9023, 0. , 0. , 0. , 0. , 0. , 0. ],
[ 0.9023, 0. , 0. , 0. , 0.9023, 1. , 0. ],
[ 0. , 0. , 0. , 0. , 0.9023, 0. , 0. ],
[ 0.9023, 0. , 0.9497, 0.857 , 0. , 0. , 0.857 ],
[ 0. , 0. , 0.9499, 0. , 0. , 0. , 0.8571],
[ 0. , 0. , 0. , 0. , 0.9023, 0.9023, 0. ]])
Die resultierende Q-Matrix ist komplexer als im einfacheren Vorgängerbeispiel. Beispiel: Ausgehend vom Flur (Zeile 1) bewegt sich der Agent in Zimmer 2 (Schlafzimmer) und von dort aus dann ins Kinderzimmer, wo die Belohnung auf ihn wartet. Ausgehend von der Küche (Zeile 4) fährt der Roboter ins Wohnzimmer (Zeile 5) von dort ins Schlafzimmer (Zeile 3) und dann schlussendlich ins Kinderzimmer.
Fazit und Ausblick
Mit Reinforcement Learning und Q-Learning ist es möglich, Algorithmen und Systeme zu entwickeln, die autark in deterministischen als auch stochastischen Umgebungen Handlungen erlernen und ausführen können; ohne diese exakt zu kennen. Dabei versucht der Agent stets basierend auf seinen Handlungen, die für ihn von der Umgebung erzeugte Belohnung zu maximieren. Dabei kann über den Diskontierungsfaktor gesteuert werden, ob der Agent einen Fokus auf kurzfristige oder langfristige Belohnungen legen soll. Die Anwendungsgebiete für solche Agenten sind vielfältig und spannend: Vor einiger Zeit veröffentlichte Google ein Paper, in dem mittels modellbasiertem Reinforcement Learning ein Agent trainiert darauf wurde, verschiedenste Atari Computerspiele zu spielen. In der nächsten Entwicklungsstufe wurde das zuvor entwickelte RL System DQN (Deep Q-Network) auf den deutlich komplexeren Strategiespiel-Klassiker StarCraft angewendet. Im Gegensatz zum hier gezeigten Beispiel wurden dabei die Ableitung der jeweils optimalen Handlung nicht in Form einer matrizenbasierten Übersicht, sondern über Deep Learning Modelle gelöst, die die Q-Werte in $s_{t+1}$ modellbasiert auf Basis der Pixel auf dem Bildschirm approximieren. Auf diesen Anwendungsfall werden wir im zweiten Teil der Reihe zum Thema Reinforcement Learning eingehen und zeigen, wie neuronale Netze und Deep Learning als Q-Approximatoren genutzt werden können. Dies eröffnet nochmals deutliche komplexere und realitätsnähere Anwendungsfälle, da die Anzahl der Stati beliebig hoch sein können.
Referenzen
- Sutton, Richard S.; Barto, Andrew G. (1998). Reinforcement Learning: An Introduction. MIT Press.
- Goodfellow, Ian; Bengio Yoshua; Courville, Cohan (2016). Deep Learning. MIT Press.


