Deep Learning – Teil 2: Programmierung


Aufbauend auf der theoretischen Einführung in neuronale Netze und Deep Learning im Rahmen des letzten Blogbeitrags, soll in Teil 2 der Reihe "Deep Learning" die Implementierung eines einfachen neuronalen Netzes (Feedforward Netz) in Python anschaulich dargestellt werden. Hierzu stehen dem Anwender viele verschiedene Frameworks zur Verfügung. In diesem Beitrag verwenden wir Keras, eine der wichtigsten Python Libraries, zur Programmierung von neuronalen Netzen und Deep Learning Modellen.
Übersicht Deep Learning Frameworks
In den letzten Jahren gab es viele Neuzugänge im Deep Learning Software-Ökosystem. Zahlreiche Frameworks, die bereits vordefinierte Bausteine zur Konstruktion von Deep Learning Netzen bieten, wurden in die Open Source Community eingeführt. Darunter sind beispielsweise das von Facebook genutzte Torch, dessen High Level Interface die Skriptsprache Lua nutzt, Caffee, das im akademischen Umfeld große Popularität genießt, Deeplearning4j, das eine Java basierte Deep Learning Umgebung bereitstellt, oder Theano, mit einem Fokus auf mathematisch effiziente Berechnungen. Neben den zuvor genannten Frameworks existieren noch viele weitere Bibliotheken, die dem Anwender die Programmierung von einfach und komplexen Deep Learning Modellen erlauben. Hierzu zählen insbesondere noch Apache MxNet oder IntelNervana NEON. Das größte und ressourcenreichste Deep Learning Frameworks ist aktuell jedoch Tensorflow, das ursprünglich vom Google Brain Team entwickelt und mittlerweile als Open Source Software veröffentlicht wurde. TensorFlow ist in C++ und Python implementiert, lässt sich jedoch auch mit kleinen oder großen Umwegen in weiteren Sprachen wie R, Julia oder Go integrieren und nutzen. Zuletzt hat sich Python vor allem aufgrund von TensorFlow sowie der darauf aufbauenden Library Keras zur Lingua Franca der Programmierung von Deep Learning Modellen etabliert.
Google TensorFlow
TensorFlow ist eine Softwarebibliothek für Python, die es erlaubt, mathematische Operationen in Form eines Graphen zu modellieren. Der Graph bildet ein Gerüst, in dessen Verlauf die Daten in jedem Knoten mathematisch transformiert an den darauf folgenden Konten weitergereicht werden. Dabei werden die Daten in sog. Tensoren gespeichert und verarbeitet. Ein Tensor ist, vereinfacht ausgedrückt, ein Container, der die im Graphen berechneten Werte speichert. Die folgende Abbildung sowie die unten stehende Python-Codebox sollen dies an einem einfachen Beispiel illustrieren:
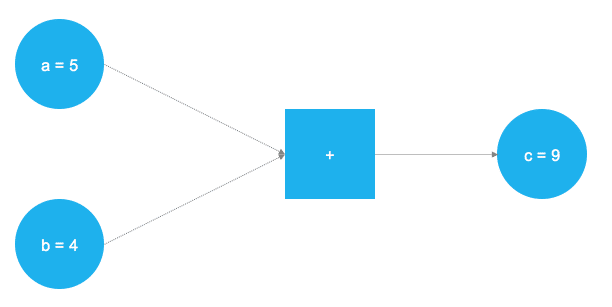
Der Graph definiert eine einfache mathematische Operation, hier eine Addition. Die Werte (Tensoren) a und b werden am quadratischen Konten des Graphen addiert und bilden den Wert c. In TensorFlow sieht das ganze dann so aus:
# TensorFlow laden
import tensorflow as tf
# a und b als Konstanten definieren
a = tf.constant(5)
b = tf.constant(4)
# Die Addition definieren
c = tf.add(a, b)
# Den Graphen initialisieren
graph = tf.Session()
# Den Graphen an der Stelle c ausführen
graph.run(c)
Das Ergebnis der Berechnung ist 9. Man sieht in diesem einfachen Beispiel schnell die grundlegende Logik hinter TensorFlow. Im ersten Schritt wird ein abstraktes Konzept des zu berechnenden Modells angefertigt (der Graph), das im folgenden Schritt mit Tensoren befüllt und an einer bestimmten Stelle ausgeführt und evaluiert wird. Natürlich sind Graphen für Deep Learning Modelle vielfach komplexer als im Minimalbeispiel oben. TensorFlow bietet dem Anwender mit der Funktion TensorBoard eine Möglichkeit, den programmierten Graphen bis ins letzte Detai zu visualisieren. Ein Beispiel für einen komplexeren Graphen sehen Sie in der unten stehen Abbildung.
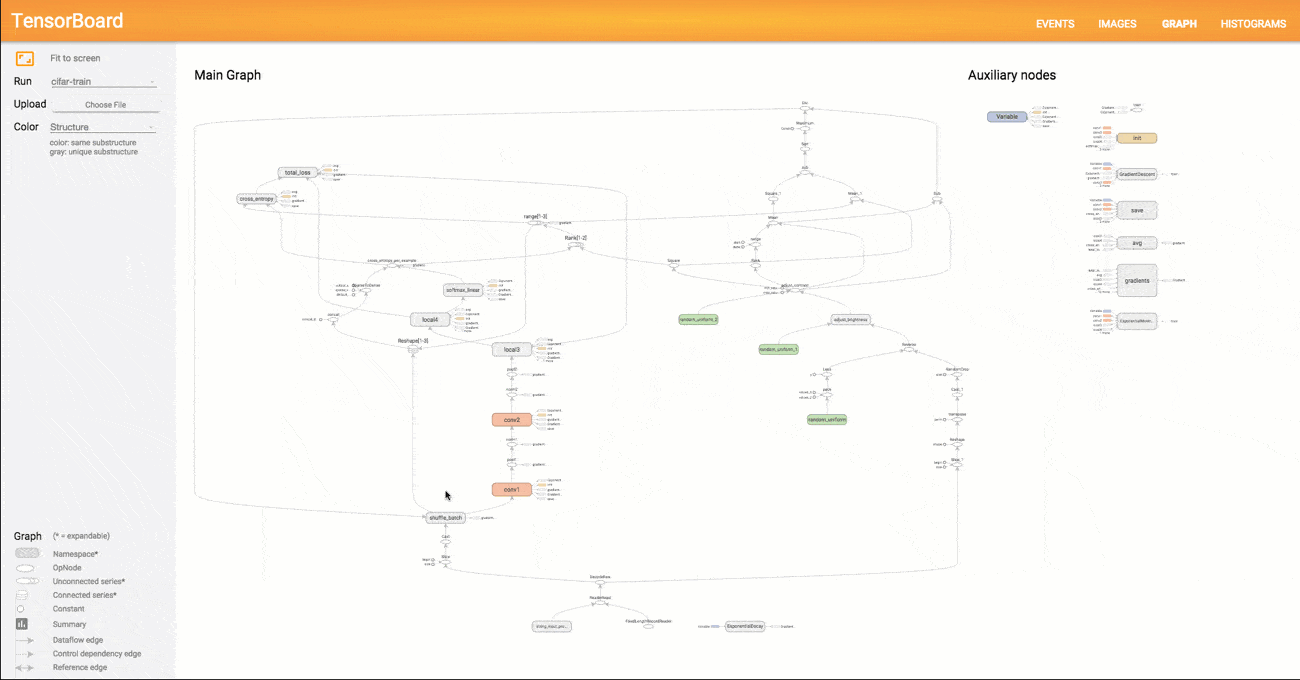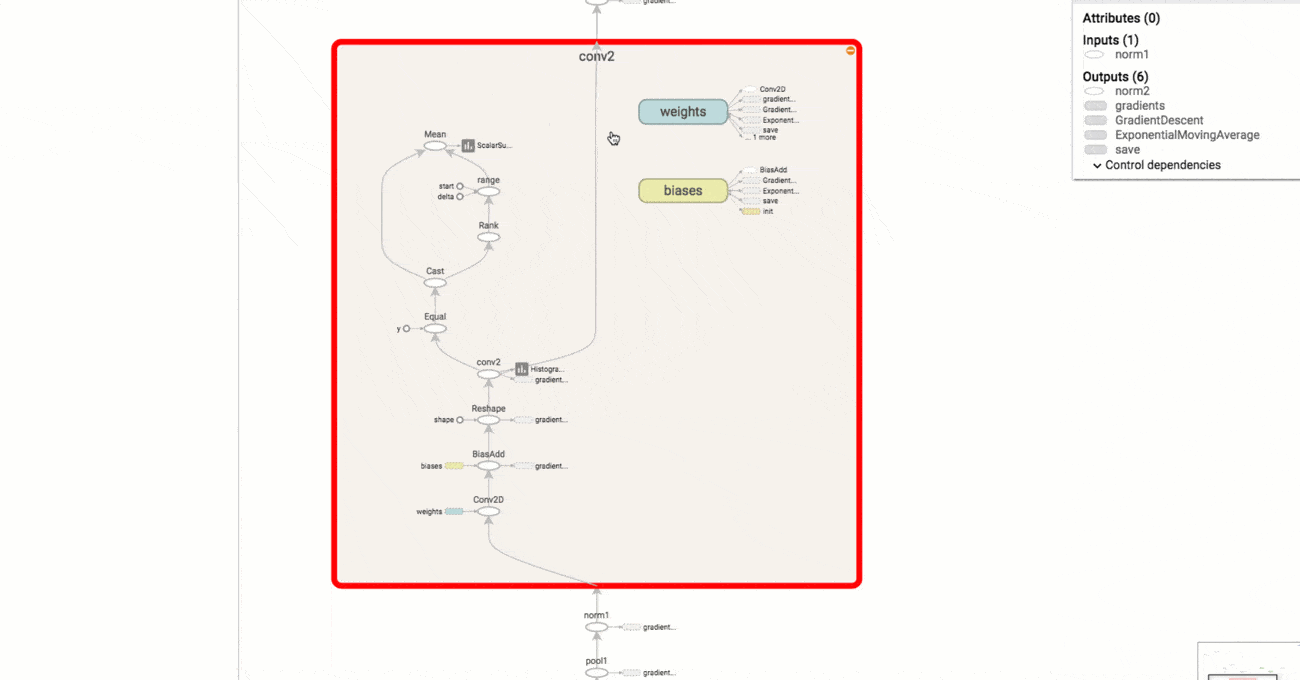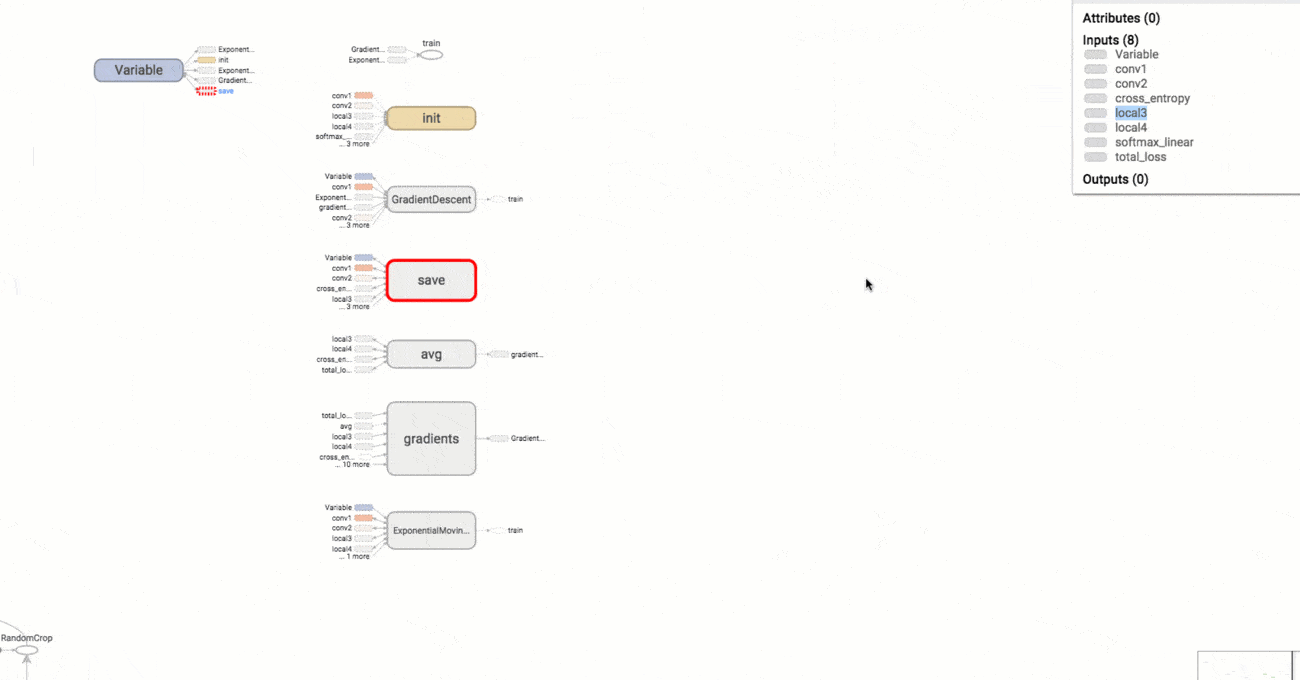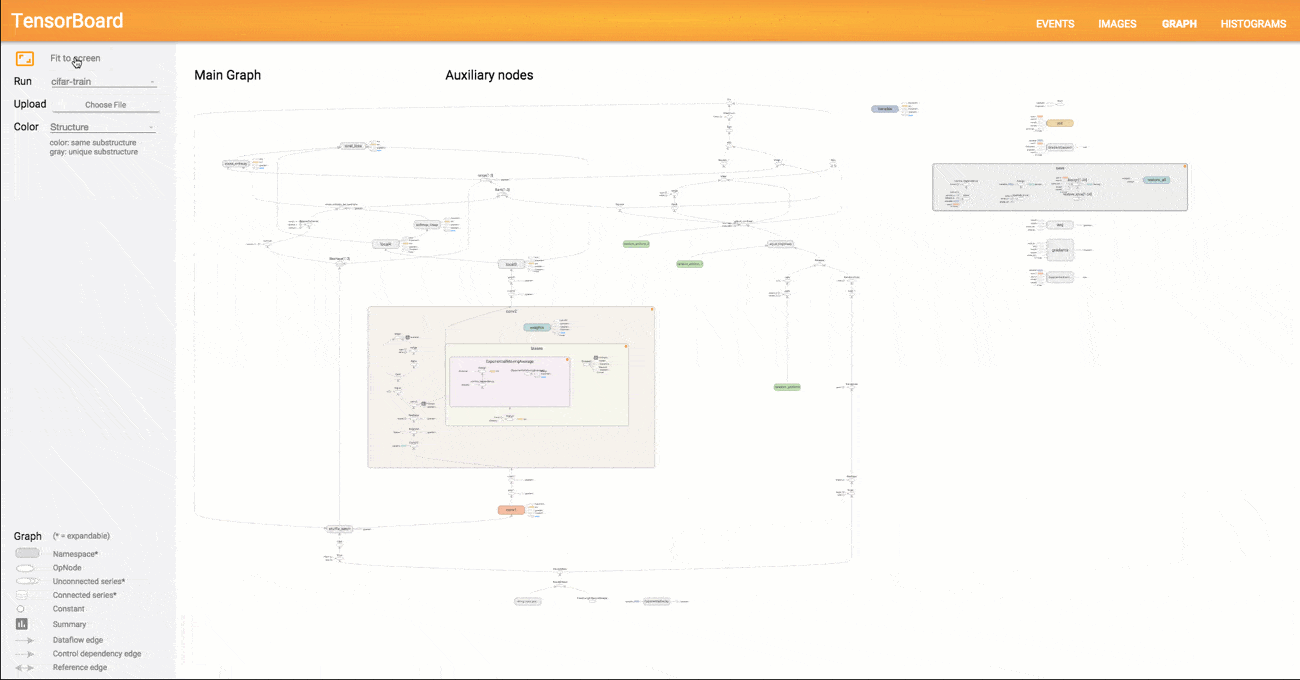
Da in TensorFlow beliebige mathematischen Operationen definiert werden können, handelt es sich streng genommen um kein reines Deep Learning Framework. Auch andere Machine Learning Modelle lassen sich als Graph repräsentieren und mit TensorFlow berechnen. Jedoch wurde TensorFlow vor allem mit Fokus auf Deep Learning entwickelt und mit zahlreichen vordefinierten Bausteinen zur Implementierung von neuronalen Netze ausgeliefert (z.B. vorgefertigte Layer für MLPs oder CNNs). Nachdem 2016 Version 1.0 veröffentlicht wurde und die Arbeit an der Tensorflow API einen wichtigen Zwischenstand erreicht hat, ist in den kommenden Jahren eine gewisse Stabilität und Konsistenz des Codes zu erwarten. Dies wird der weiteren Verbreitung von TensorFlow und dem Einsatz in Produktivsystemen weiter zugutekommen. Neben der Python Library existiert auch ein TensorFlow Server, der für den Einsatz in Unternehmen konzipiert wurde und fertige TensorFlow Modelle als Service bereitstellt.
Einführung in Keras
TensorFlow ist trotz der bereits angesprochenen, vorgefertigten Blöcke immer noch ein Expertensystem und erfordert für den Anwender eine hohe Einarbeitungszeit. Die relative Entwicklungszeit von der ersten Idee bis hin zum fertigen Deep Learning Modell ist in TensorFlow extrem lang - jedoch auch maximal flexibel.
Die langwierige Explorationszeit in den meisten Deep Learning Frameworks soll durch Keras, einem einfach zu bedienenden Interface zur Erstellung von Deep Learning Modellen, abgemildert werden. Keras vereinfacht mithilfe einer simpleren Syntax die Konzeption, das Training und die Evaluierung von Deep Learning Modellen. Keras arbeitet grundsätzlich auf der Abstraktionsebene der einzelnen Schichten des neuronalen Netzes und verbindet diese in der Regel bereits automatisch. Detailfragen zur Netzarchitektur bzw. zur Implementierung selbiger entfallen größtenteils. So können einfache Standardmodelle wie MLPs, CNNs und RNNs schnell und effektiv prototypisiert werden. Das Besondere an Keras ist, dass es kein eigenes Backend für Berechnungen bereitstellt, sondern lediglich die vereinfachte Nutzung darunterliegender Bibliotheken wie TensorFlow, Theano oder CNTK ermöglicht. Ein Vorteil hiervon ist, dass der Code zur Spezifikation der Netzarchitekturen dabei für alle Backends gleich ist und von Keras automatisch "übersetzt" wird. Dies erlaubt eine extrem schnelle Entwicklung in verschiedenen Frameworks ohne sich in die komplexe Syntax der Backends einarbeiten zu müssen. Dementsprechend ist der Code sowohl deutlich kürzer als auch besser lesbar im Vergleich zu dem entsprechenden Pendant in der Original-Syntax des verwendeten Frameworks.
Beispiel: Implementierung eines neuronalen Netzes
Im Rahmen der folgenden Codebeispiele zur Implementierung von Deep Learning Modellen wird die Python API von Keras verwendet. Das folgende Beispiel befasst sich mit der Vorhersage des S&P500 Kurses für die jeweils nächste Handelsminute auf Basis der Kurse der enthaltenen Aktientitlel im Index. Das Beispiel dient lediglich zur Veranschaulichung der Implementierung eines neuronalen Netzes und ist nicht auf Performance optimiert (es sei an dieser Stelle angemerkt, dass die Prognose von Aktien- und Indexkursen nach wie vor extrem schwierig ist, insbesondere je kleinteiliger die Zeitintervalle werden. Einen interessanten Approach zur Ensemble-Prognose von Aktien verfolgt der AI-Fonds NUMERAI). Die Datenbasis für das Modelltraining besteht aus den Kursen der Underlyings und des Index in Handelsminuten im Zeitraum April – Juli 2017. Jede Zeile des Trainingsdatensatzes beinhaltet somit die Kurse aller Indextitel als Features für die Vorhersage sowie dem Indexkurs der nächsten Minute als Target. Der Testdatensatz besteht aus den gleichen Daten für den Monat August 2017.Im folgenden Abschnitt wird die Python Modellspezifikation in Keras erläutert. Dabei wird angenommen, dass die DataFrames, die die Trainings- und Testdaten beinhalten bereits vorliegen:
# Layer aus der Keras Bibliothek laden
from keras.layers import Dense
from keras.models import Sequential
Zuerst werden die notwendigen Komponenten aus Keras importiert. Hier sind dies die Klassen für einen voll verbundenen Layer (Dense) und der Typ des Modells (Sequential), sowie die Hauptbibliothek für die Berechnungen.
# Initialisierung eines leeren Netzes
model = Sequential()
# Hinzufügen von 2 Feedforward Layern
model.add(Dense(512, activation="relu", input_shape=(ncols,)))
model.add(Dense(256, activation="relu"))
# Output Layer
model.add(Dense(1))
Zunächst wird das Gerüst des Modells in einem Objekt definiert (model). Nachdem der Container für das Modell instanziert wurde, werden diesem zwei Hidden Layer mit 512 bzw. 256 Neuronen und der ReLu Aktivierungsfunktion hinzugefügt. Die letzte Schicht im Modell, der Output Layer, summiert die zuvor berechneten Outputs der vorangehenden Knoten auf und gewichtet diese entsprechend.
# Modell kompilieren
model.compile(optimizer="adam", loss="mean_squared_error")
# Modell trainieren mit den Trainingsdaten
model.fit(x=stockdata_train_scaled,
y=stockdata_train_target,
epochs=100, batch_size=128)
# Geschätztes Modell auf den Testdaten evaluieren
results = model.evaluate(x=stockdata_test_scaled, y=stockdata_test_target)
Nach der Definition der Netzarchitektur wird das Netz zusammen mit den Trainingsparametern kompiliert. Da es sich bei diesem Beispiel um ein Regressionsproblem handelt, wird hier der Mean Squared Error (MSE) als Kostenfunktion verwendet. Der MSE berechnet in jeder Iteration die mittlere quadratische Abweichung zwischen den tatsächlich beobachteten und durch das Netz vorhergesagten Werten. Während des Trainings wird der MSE iterativ durch ein adaptives Gradientenverfahren (ADAM) minimiert. Mittels "Backpropagation" werden die Gewichtungen zwischen den Neuronen so angepasst, dass in jeder Iteration der MSE niedriger wird (bzw. werden sollte). Im vorliegenden Beispiel wurden 100 Epochen als Trainingszeit gewählt, jedoch sollte in einem realen Anwendungsfall auch dieser Parameter durch ausgiebige Tests optimiert werden. Eine Epoche entspricht einem kompletten Durchlauf der Daten, d.h. das Netz hat jeden Datenpunkt der Trainingsdaten einmal "gesehen".
Ergebnis und Ausblick
Wie die folgende Abbildung zeigt, ist das Ergebnis nicht ideal. Die blaue Linie zeigt die tatsächlichen S&P500 Indexwerte, die Schätzung durch das Modell ist in orange dargestellt.
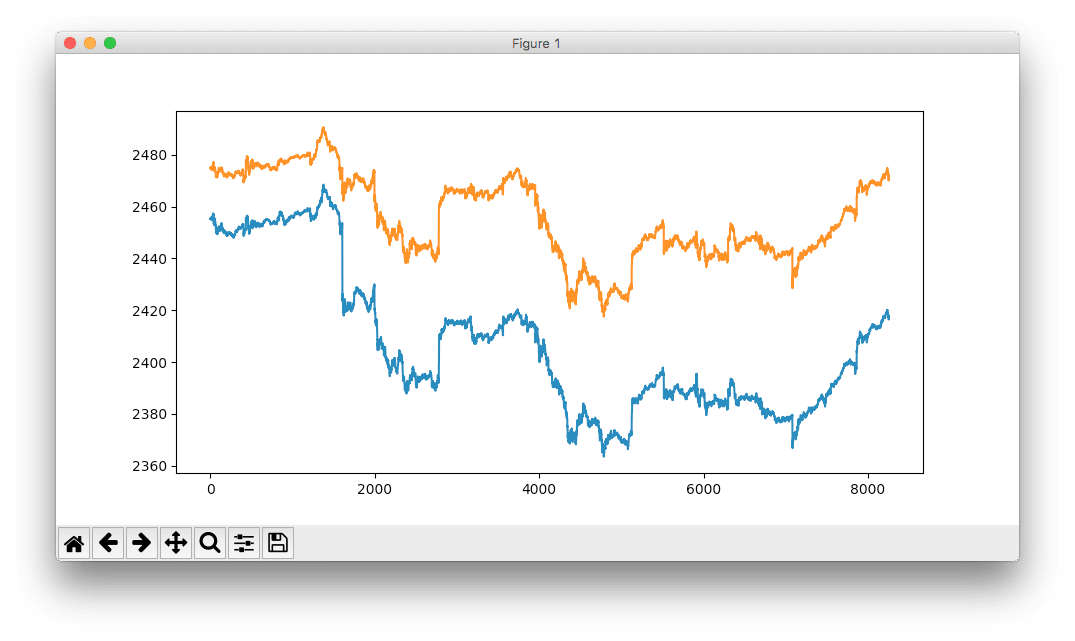
Interessant ist, dass bereits das nicht optimierte Netz die Struktur des Verlaufs gelernt hat, auch wenn die Ausschläge und Effekte noch massiv überschätzt werden.
In nächsten Beitrag aus der Reihe "Deep Learning" setzen wir an dieser Stelle an und werden die Performance unseres Modells durch die Anwendung verschiedener Tuningansätze weiter verbessern. Christian Moreau Christian Moreau


