Deep Learning – Teil 1: Einführung


Deep Learning ist aktuell einer der spannendsten Forschungsbereiche im Machine Learning. Für eine Vielzahl von Fragestellungen liefern Deep Learning Modelle State-of-the-Art Ergebnisse, vor allem im Bereich der Bild-, Sequenz- und Spracherkennung. Weiterhin findet Deep Learning erfolgreich Anwendung in der Fahrzeugkonstruktion (selbstfahrende Autos), in der Finanzwelt (Aktienkursvorhersage, Risikoprognose, automatische Handelssysteme), in der Medizin (maschinelle Bilderkennung von Karzinomen) und Biologie (Genomik), im e-Commerce (Recommendation Systeme) und im Web Umfeld (Anomalieerkennung).
Wie unterscheidet sich Deep Learning von klassischen Machine Learning Algorithmen und warum funktioniert es bei vielen Fragestellungen so gut? Dieser Artikel soll Ihnen eine Einführung in die Grundkonzepte von Deep Learning geben und Unterschiede zu klassischen Verfahren aus dem Machine Learning herausarbeiten.
Einführung in neuronale Netze
Deep Learning erscheint dem Anwender auf den ersten Blick als eine relative neue Methodik. Dies ist hauptsächlich darin begründet, dass die generelle Aufmerksamkeit rund um das Thema durch die vielen methodischen Durchbrüche in den letzten Jahren nicht abzureißen scheint. Fast täglich erscheinen neue wissenschaftliche Publikationen zum Thema Deep Learning bzw. zu angrenzenden Forschungsbereichen.
Fakt ist jedoch, dass die theoretischen und methodischen Grundlagen für Deep Learning durch die wissenschaftliche Entwicklung von neuronalen Netzen bereits vor vielen Jahrzehnten in der 1950er Jahren gelegt wurden. Aufgrund verschiedener technischer und methodischer Limitationen waren damals wirkliche "Netze", die aus hunderten oder tausenden von Elementen bestehen noch in weiter Ferne. Zunächst beschränkte sich die Forschung auf einzelne Einheiten neuronaler Netze, das Perzeptron bzw. Neuron. Als Vorreiter auf diesem Gebiet ist Frank Rosenblatt zu nennen, der während seiner Zeit am Cornell Aeronautical Laboratory 1957 bis 1959 ein einzelnes Perzeptron bestehend aus 400 photosensitiven Einheiten (Inputs), die über eine "Zuordnungsschicht" (Association Layer) mit einer Ausgabeschicht von 8 Einheiten verbunden waren. Heute gilt das Rosenblatt Perzeptron als die Geburtsstunde von neuronalen Netzen und Deep Learning Modellen.[caption id="attachment_12724" align="aligncenter"]

Frank Rosenblatt (links) bei der Arbeit am Mark I Perceptron.[/caption]Selbst Jahrzehnte später in den 1980er Jahren, als neuronale Netze ein erstes gesteigertes Interesse erfuhren, blieben tatsächliche praktische Erfolge eher überschaubar. Andere Algorithmen, bspw. Kernel Methoden (Support Vector Machines) oder Decision Trees verdrängten neuronale Netze in den 80er und 90er Jahren auf die hinteren Plätze der Machine Learning Rangliste. Zum damaligen Zeitpunkt konnten neuronale Netze ihr volles Potenzial noch nicht entfalten. Zum einen fehlte es noch immer an Rechenpower, zum anderen litten komplexere Netzarchitekturen, so wie sie heute verwendet werden, am sog. "Vanishing Gradient Problem", welches das ohnehin schon schwierige Training der Netze weiter erschwerte oder gänzlich unmöglich machte. Bis in die Anfänge des neuen Jahrtausends fristeten die heute umjubelten neuronale Netze ein weitestgehend tristes Dasein im stillen Kämmerlein.
Erst als Geoffrey Hinton, einer der renommiertesten Forscher im Bereich neuronaler Netze, im Jahr 2006 ein revolutionäres Paper veröffentlichte in dem erstmalig das erfolgreiche Training eines mehrschichtigen neuronalen Netzes gelang, erfuhr das Thema neue Beachtung in Forschung und Praxis. Neue methodische Fortschritte, bspw. die Spezifikation von alternativen Aktivierungsfunktionen, die das Vanishing Gradient Problem verhindern sollten oder die Entwicklung von verteilten Rechensystemen beflügelten die Forschung und Anwendung im Bereich neuronaler Netze. Seit nun mehr als 10 Jahren etablieren sich neuronale Netze und Deep Learning zusehends als Synonym für maschinelles Lernen und künstliche Intelligenz. Sie sind ein boomendes wissenschaftliches Forschungsfeld und finden in vielen Praxisszenarien Anwendung. Regelmäßig unterbieten sich Deep Learning Modelle bei der Lösung komplexer Machine Learning Aufgaben im Bereich Sprach- und Bilderkennung. Getrieben durch die rasanten technischen Fortschritte im Bereich verteiltes Rechnen und GPU Computing scheint es nun so, als wäre Deep Learning schlussendlich zur richtigen Zeit am richtigen Ort, um sein volles Potenzial zu entfalten.
Neuronale Netze - ein Abbild des Gehirns?
Entgegen der weit verbreiteten Meinung, dass neuronale Netze auf der Funktionsweise des Gehirns basieren, kann lediglich bestätigt werden, dass sich moderne Deep Learning Modelle nur zu einem gewissen Teil aus Erkenntnissen der Neurowissenschaft entwickelten. Zudem weiß man heute, dass die tatsächlichen Abläufe und Funktionen im Gehirn, die zur Verarbeitung von Informationen berechnet werden, wesentlich komplexer sind als in neuronalen Netzen abgebildet. Grundsätzlich kann jedoch die Idee, dass viele einzelne "Recheneinheiten" (Neuronen) durch eine Vernetzung untereinander Informationen intelligent verarbeiten als Grundprinzip anerkannt werden.
Im Gehirn sind Neuronen über Synapsen miteinander verbunden, die sich zwischen Neuronen neu bilden bzw. allgemein verändern können. Die unten stehende Abbildung zeigt eine Pyramidenzelle, eine der am häufigsten anzutreffenden Neuronenstrukturen im menschlichen Gehirn.[caption id="attachment_12727" align="aligncenter" ]

Darstellung einer Pyramidenzelle (Abbildung aus Haykin, Simon (2008), Seite 8)[/caption]Wie auch andere Neuronenarten empfängt die Pyramidenzelle die meisten Ihre Eingangssignale über die Dendriten, die mittels Axon und dessen Dendriten zehntausend oder mehr Verbindungen zu anderen Neuronen eingehen können. Gemäß dem sog. Konvergenz-Divergenzprinzip erfolgt die Erregung einzelner Neuronen auf Basis vieler anderer Zellen wobei das Neuron ebenfalls gleichzeitig Signale an viele andere Zellen aussendet. Somit entsteht ein hochkomplexes Netzwerk von Verbindungen im Gehirn, die zur Informationsverbeitung genutzt werden.
Einfach gesprochen, verarbeiten im Gehirn somit einzelne Neuronen die Signale anderer Neuronen (Inputs) und geben ein darauf basierendes, neues Signal an die nächste Gruppe von Neuronen weiter. Ein einzelnes Neuron ist somit durch eine bestimmte biologische (bzw. mathematische) Funktion repräsentiert, die seine Eingangssignale bewertet, ein entsprechendes Reaktionssignal erzeugt und dieses im Netzwerk an weitere Neuronen weitergibt. Der Begriff Netzwerk entsteht dadurch, dass viele dieser Neuronen in Schichten zusammengefasst werden und Ihre Signale die jeweils folgenden Knoten bzw. Schichten weitergeben und sich somit ein Netz zwischen den Neuronen spannt.
Was versteht man unter Deep Learning?
Unter Deep Learning versteht man heute Architekturen von neuronalen Netzen, die über mehr als einen Hidden Layer verfügen. Der Nutzen mehrerer Neuronen-Schichten macht sich dadurch bemerkbar, dass zwischen den Schichten "neue" Informationen gebildet werden können, die eine Repräsentation der ursprünglichen Informationen darstellen. Wichtig hierbei ist zu verstehen, dass diese Repräsentationen eine Abwandlung bzw. Abstaktion der eigentlichen Eingangssignale sind.
"Unter Deep Learning versteht man heute neuronalen Netze, die über mehr als einen Hidden Layer verfügen."
Dieser Mechanismus, der unter dem Begriff "Representation Learning" zusammengefasst werden kann sorgt dafür, dass Deep Learning Modelle in der Regel sehr gut auf neue Datenpunkte abstrahieren können. Der Grund dafür ist, dass die geschaffenen Abstraktionen der Daten wesentlich generellerer Natur als es die ursprünglichen Eingangsdaten sind. Lernen durch Repräsentation ist bei Deep Learning eines der Hauptunterscheidungsmerkmale gegenüber klassischen Machine Learning Modellen, die i.d.R. ohne Repräsentation der Daten lernen. Die folgende Abbildung illustriert den Unterschied zwischen statistischen Computerprogrammen (Rule-based Systems), klassischen Machine Learning Modellen und Deep Learning.[caption id="attachment_11479" align="aligncenter" ]

Schematische Darstellung Representation Learning (Abbildung aus Goodfellow (2016), Seite 10)[/caption]Da Deep Learning Modelle theoretisch über sehr viele Schichten verfügen, ist die Abstraktionskapazität besonders hoch. Somit kann ein Deep Learning Modell auf verschiedenen Ebenen Abstraktionen der Eingangsdaten bilden und zur Lösung des Machine Learning Problems verwenden. Ein Beispiel für eine solche komplexe Architektur ist das GoogleNet zur Bildklassifikation (siehe Abbildung).[caption id="attachment_11482" align="aligncenter" ]

Übersicht Architektur GoogleNet.[/caption]Das GoogleNet verfügt über mehrere Architekturblöcke, die speziell auf die Anforderungen im Bereich Objekt- bzw. Bilderkennung ausgelegt sind. Somit ist das Netz in der Lage durch Representation Learning mehrere tausend Objekte auf Bildern mit einer hohen Genauigkeit zu erkennen.
Aufbau und Bestandteile von neuronalen Netzen
Zurück zu den Basics. Der Grundbaustein jedes neuronalen Netzes ist das Neuron. Ein Neuron ist ein Knotenpunkt im neuronalen Netzwerk an dem ein oder mehrere Eingangssignale (numerische Daten) zusammentreffen und von der sog. Aktivierungsfunktion des Neurons weiterverarbeitet werden. Der Output des Neurons ist somit eine Funktion des Inputs. Es existieren verschiedene Aktivierungsfunktionen, auf die wir in späteren Teilen unserer Deep Learning Reihe genauer eingehen werden.
Der elementare Grundbaustein jedes neuronalen Netzes ist das Neuron. Ein Neuron ist ein Knotenpunkt im neuronalen Netzwerk an dem ein oder mehrere Eingangssignale (Inputs) zusammentreffen und verarbeitet werden. Dabei kann es sich, je nachdem an welcher Stelle sich das Neuron im Netzwerk befindet, sowohl um Signale der Eimngangsschicht als auch Signale vorhergehender Neuronen handeln. Nach der Verarbeitung der Eingangssignale werden diese als Output an die nachfolgenden Neuronen weitergegeben. Formal gesprochen, ist der Output eines Neurons eine Funktion der Inputs. Die folgende Abbildung soll den grundsätzlichen Aufbau darstellen:
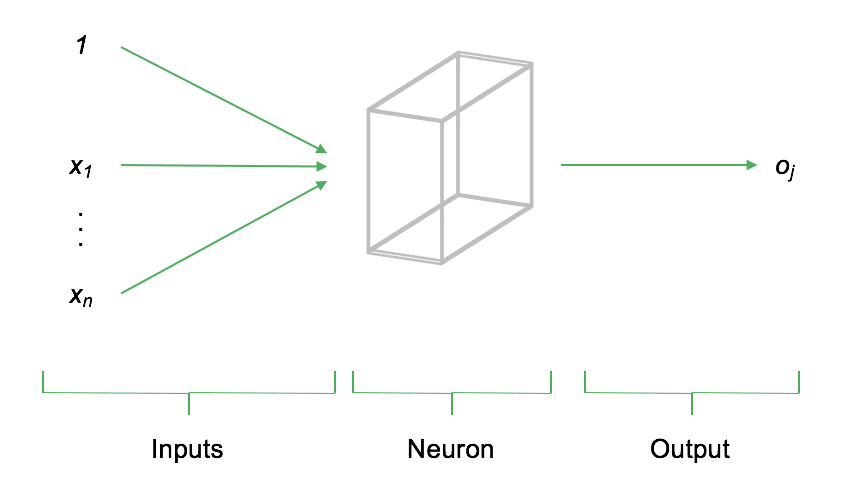
Die obenstehende Abbildung stellt schematisch den Aufbau eines einzelnen Neurons dar. Auf der linken Seite der Abbildung treffen die Inputs x_1,...,x_n am Neuron ein. Input steht dabei für einen beliebigen numerischen Wert (z.B. vorhandene Daten oder Signale vorhergehender Neuronen). Das Neuron bewertet (gewichtet) den Input, berechnet den Output o_j und gibt diesen an die darauffolgenden, verbundenen Neuronen weiter. Der Input eines Neurons ist somit die gewichtete Summe aller mit ihm verknüpften vorher liegenden Neuronen.
In der Regel werden in neuronalen Netzen keine einzelnen Neuronen, sondern ganze Schichten mit beliebig vielen dieser Knoten, modelliert. Diese Schichten werden "Hidden Layer" genannt und sind der Kern der Architektur von Deep Learning Modellen. Analog zum Hidden Layer existieren der Input- und Output Layer. Ersterer ist der Eintrittspunkt der Daten in das Modell, während letzterer das Ergebnis des Modells repräsentiert. In einer einfachen Architektur sind alle Neuronen aller benachbarten Layer miteinander verbunden. Die folgende Abbildung stellt den Aufbau eines einfachen neuronalen Netzes mit einem Input Layer, einem Hidden Layer und einem Output Layer dar.
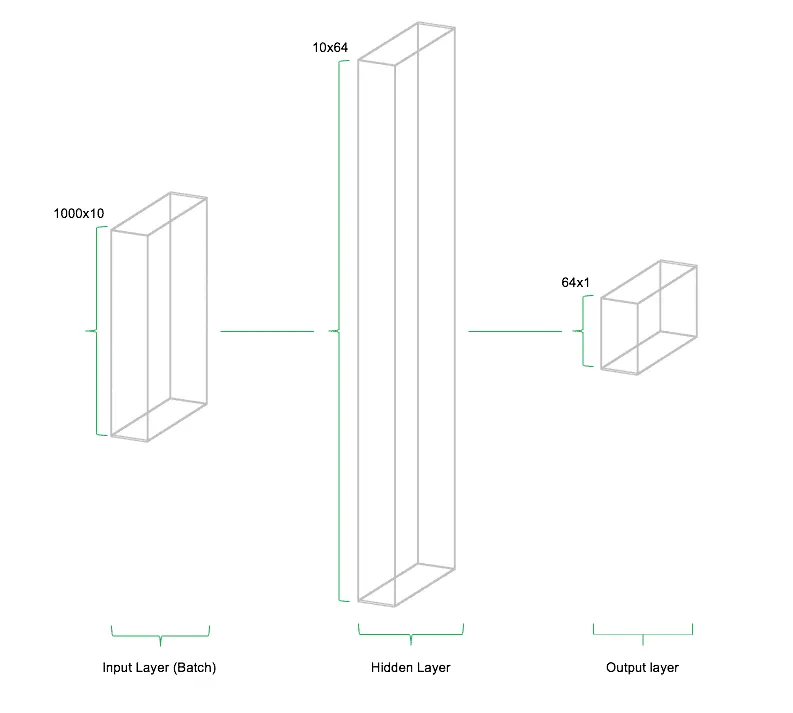
Die Verbindungen (Gewichte / Weights) zwischen den Neuronen sind derjenige Teil des neuronalen Netzes, der auf die vorliegenden Daten angepasst wird. Die Architektur des Netzes bleibt (zumindest in einfachen Architekturen) konstant während des Trainings. Die Gewichte werden von Iteration zu Iteration so angepasst, dass der Fehler, den das neuronale Netz während dem Trainings macht immer weiter reduziert wird. Während des Trainings werden Abweichungen der Schätzung des Netzwerks von den tatsächlich beobachteten Datenpunkten berechnet. Nach der Berechnung des Gesamtfehlers werden die Gewichte des Netzes rekursiv aktualisiert. Die Richtung dieser Aktualisierung wird so gewählt, dass der Fehler im nächsten Durchlauf kleiner wird. Diese Methodik nennt man "Gradient Descent" und beschreibt die iterative Anpassung der Modellparameter in entgegengesetzter Richtung zum Modellfehler. Auch heutzutage werden Deep Learning Modelle und neuronale Netze mittels Gradient Descent bzw. aktuelleren Abwandlungen davon trainiert.
Architekturen von neuronalen Netzen
Die Architektur von neuronalen Netzen kann durch den Anwender nahezu frei spezifiziert werden. Tools wie TensorFlow oder Theano ermöglichen es dem Anwender, Netzarchitekturen beliebiger Komplexität zu modellieren und auf den vorliegenden Daten zu schätzen. Zu den Parametern der Netzarchitektur zählen im einfachsten Falle die Anzahl der Hidden Layer, die Anzahl der Neuronen pro Layer sowie deren Aktivierungsfunktion. Im Rahmen der Forschung zu neuronalen Netzen und Deep Learning haben sich unterschiedlichste Architekturen von Netzwerken für spezifische Anwendungen entwickelt. Jede dieser Architekturen weist spezifische Vorteile und Eigenschaften auf, die die Verarbeitung von speziellen Informationen erleichtern sollen. So wird beispielsweise bei Convolutional Neural Networks (CNNs), die primär zur Verarbeitung von Bildinformationen eingesetzt werden, die räumliche Anordnung von Informationen berücksichtigt, bei Recurrent Neural Nets (RNNs) die zeitliche Anordnung von Datenpunkten. Im Folgenden sollen die wichtigsten Typen von Architekturen kurz skizziert werden.
Feedforward Netze
Unter einem Feedforward Netz versteht man ein neuronales Netz mit einer Inputschicht, einem oder mehreren Hidden Layers sowie einer Outputschicht. In der Regel handelt es sich bei den Hidden Layers um sogenannte "Dense Layers", d.h. voll vernetzte Neuronen mit Gewichtungen zu allen Neuronen der vorherigen und folgenden Schicht. Die folgende Abbildung zeigt ein Deep Learning Modell, das mit vier Hidden Layers konstruiert wurde.

Während Multi Layer Perceptrons (MLP) als universale Architekturen für eine Vielzahl von Fragestellungen geeignet sind, weisen Sie einige Schwächen in bestimmte Einsatzgebieten auf. So steigt die für eine Bildklassifikation notwendige Anzahl der Neuronen für eine Bildklassifikation mit jedem Pixel des Bildes immer weiter an.
Convolutional Neural Networks (CNNs)
Convolutional Neural Networks (CNN) sind ein spezieller Typ von neuronalen Netzwerken zur Verarbeitung von räumlich angeordneten Daten. Hierzu zählen bspw. Bildinformationen (2 Dimensionen), Videos (3 Dimensionen) oder Audiospuren (1-2 Dimensionen). Die Architektur von CNNs unterscheidet sich deutlich von der eines klassischen Feedforward Netzes. CNNs werden mit einer speziellen Architektur gestaltet, den sogenannten Convolutional und Pooling Layers. Der Zweck dieser Schichten ist die Untersuchung des Inputs aus verschiedenen Perspektiven. Jedes Neuron im Convolutional Layer überprüft einen bestimmten Bereich des Input Feldes mithilfe eines Filters, dem sog. Kernel. Ein Filter untersucht das Bild auf eine bestimmte Eigenschaft, wie z.B. Farbzusammensetzung oder Helligkeit. Das Ergebnis eines Filters ist der gewichtete Input eines Bereichs und wird im Convolutional Layer gespeichert.

Die Größe (oder vielmehr Tiefe) des Convolutional Layers definiert sich über die Anzahl der Filter, da jeweils das gesamte Input Bild von jedem Filter geprüft wird. Diese Information wird zwischen den einzelnen Convolutional Layern mit sogenannten Pooling Layern komprimiert. Die Pooling Layer laufen die, durch die Filter erstellten, Feature Maps ab und komprimieren diese, d.h. sie reduzieren die Anzahl der Pixel nach einer gegebenen Logik weiter. Beispielsweise können hierbei Maximalwerte oder Mittelwerte der Filter verwendet werden. Anschließend können noch weitere Convolutional Layer und/oder Pooling Schichten folgen, bis die abstrahierten Features in ein voll vernetztes MLP übergeben werden, das wiederum im Output Layer mündet und die Schätzungen des Modells berechnet. Convolutional und Pooling Layer komprimieren somit die räumlich angeordneten Informationen und reduzieren die Anzahl der geschätzten Gewichtungen im Netzwerk. Somit können auch hochdimensionale Bilder (hohe Auflösung) als Inputs verwendet werden.
Recurrent Neural Networks (RNNs)
Recurrent Neural Networks (RNNs) sind ein Oberbegriff für eine Gruppe von Netzwerkarchitekturen bei denen die Neuronen ihre Signale in einem geschlossenen Kreis weitergeben. Dies bedeutet, dass der Output einer Schicht auch an die gleiche Schicht als Input zurückgegeben wird. Es ist dem Netzwerk dadurch möglich Informationen bzw. Daten aus zeitlich weit auseinanderliegende Observationen im Training mit zu berücksichtigen. Dadurch eignet sich diese Architekturform primär für die Analyse sequentieller Daten, wie etwa Sprache, Text oder Zeitreihendaten.
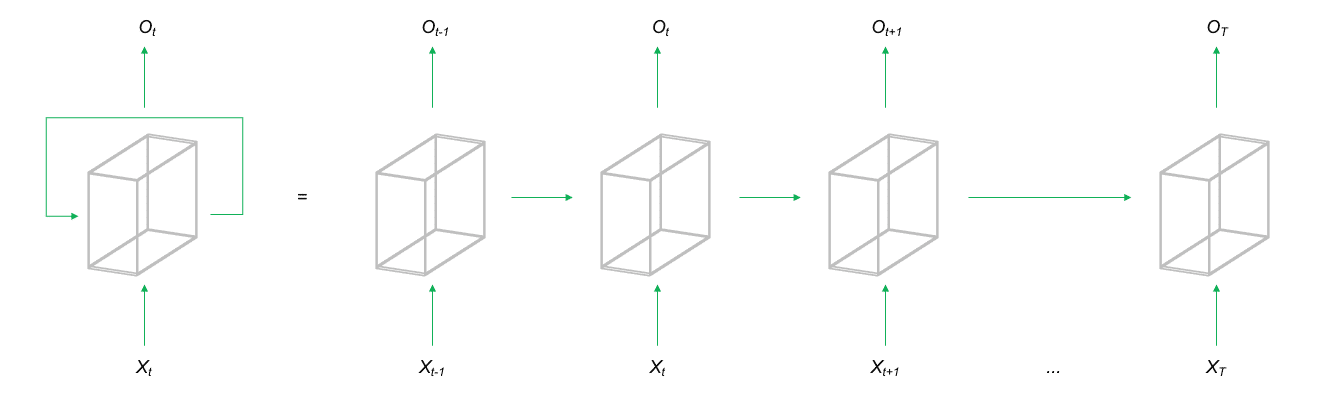
Eine der bekanntesten RNN Architekturen ist das Long Short Term Memory (LSTM) Netzwerk. Hierbei werden zusätzliche Parameter darauf trainiert, den Input und Output des Netzes für die nächste Iteration zu speichern oder zu verwerfen, um auf diese Weise zusätzliche Informationen zur Vorhersage für den nächsten Sequenzabschnitt zur Verfügung zu stellen. So können zuvor aufgetretene Signale über die zeitliche Dimension der Daten gespeichert und später verwendet werden. LSTMs werden aktuell sehr erfolgreich im NLP (Natural Language Processing) angewendet, um Übersetzungen von Texten anzufertigen oder Chat-Bots zu trainieren. Weiterhin eignen sich RNNs für die Modellierung von Sequenzen im Allgemeinen, bspw. bei der Zeitreihenprognose oder aber auch für Next Best Action Empfehlungen.
Weitere Netzarchitekturen
Neben den drei oben dargestellten Architekturen für Deep Learning Modelle existieren zahlreiche Varianten und Abwandlungen von CNNs und RNNs. Weiterhin erfahren aktuell sog. GANs (Generative Adversarial Networks) große Aufmerksamkeit in der Deep Learning Forschung. GANs werden verwendet, um Inputs des Modells zu synthetisieren, um somit neue Datenpunkte aus der gleichen Wahrscheinlichkeitsverteilung der Inputs zu generieren. So lassen sich zum Beispiel Datensätze aber auch Bild- und Toninformationen erzeugen, die dem gleichen "Stil" der Inputs entsprechen. Somit können z.B. neue Texte, die in ihrer Komposition denen bekannter Schriftsteller entsprechen oder neue Kunstwerke, die dem Malstil großer Künstler nachempfunden sind erzeugt werden.

Die Anwendungsbereiche von GANs sind extrem spannend und zukunftsträchtig, jedoch ist aktuell das Training solcher Netze noch experimentell und noch nicht ausreichend gut erforscht. Erste Modelle und Ergebnisse aus der aktuellen Forschung sind jedoch äußerst vielversprechend. Spannende Ergebnisse werden insbesondere im Bereich der künstlichen Bilderzeugung generiert. So werden heute bereits GANs trainiert, die es ermöglichen anhand eines Fotos das Aussehen im hohen Alter zu simulieren oder anhand einer Frontalaufnahme eine 360-Grad-Ansicht des Motivs zu generieren. Weitere Anwendung finden GANs im Bereich Text-t0-Image Synthese, d.h. anhand einer textualen Bildbeschreibung erzeugt das GAN eine fotorealistische Abbildung.
Zusammenfassung und Ausblick
Deep Learning und neuronale Netze sind spannende Machine Learning Methoden, die auf eine Vielzahl von Fragestellungen angewendet werden können. Durch Representation Learning, also der Fähigkeit abstrakte Konzepte aus Daten zu extrahieren und diese zur Lösung eines Problems zu verwenden, zeigen Deep Learning Modelle für viele komplexe Fragestellungen eine hohe Genauigkeit und Generalisierbarkeit auf neue Daten. Die Entwicklung von Deep Learning Modellen, Algorithmen und Architekturen schreitet extrem schnell voran, sodass davon ausgegangen werden kann, dass sich Deep Learning weiter als Benchmark in vielen Machine Learning Disziplinen festigen wird. Durch die immer weitere voranschreitende technische Entwicklung kann damit gerechnet werden, dass immer komplexere Architekturen modelliert werden können. Bereits heute gibt es spezielle Deep Learning Hardware, wie Google TPUs (Tensor Processing Units), die speziell auf die numerischen Anforderungen von Deep Learning Modellen abgestimmt sind.
Referenzen
- Rosenblatt, Frank (1958). The perceptron. A probabilistic model for information storage and organization in the brain. Psychological Reviews, 65: S. 386–408.
- Goodfellow, Ian; Bengio Yoshua; Courville, Cohan (2016). Deep Learning. MIT Press.
- Haykin, Simon (2008). Neural Networks and Machine Learning. Pearson.
- Bishop, Christopher M (1996). Neural Networks for Pattern Recognition. Oxford Press.
[author class="mtl" title="Über den Autor"]


