Deep Learning - Part 1: Introduction

Deep Learning is currently one of the most exciting research areas in machine learning. For a wide range of problems, deep learning models deliver state-of-the-art results, especially in the fields of image, sequence, and speech recognition. Furthermore, deep learning is successfully applied in vehicle engineering (self-driving cars), finance (stock price prediction, risk forecasting, automated trading systems), medicine (machine-based image recognition of carcinomas), biology (genomics), e-commerce (recommendation systems), and web environments (anomaly detection). How does deep learning differ from traditional machine learning algorithms, and why does it perform so well for many problems? This article aims to introduce you to the fundamental concepts of deep learning and highlight the differences from traditional machine learning methods.

Introduction to Neural Networks

At first glance, deep learning appears to be a relatively new methodology. This perception is mainly due to the continuous attention the field has received, driven by numerous methodological breakthroughs in recent years. Almost daily, new scientific publications emerge on deep learning and related research areas. However, the fact remains that the theoretical and methodological foundations of deep learning were established decades ago, in the 1950s, through the scientific development of neural networks. Due to various technical and methodological limitations at the time, real "networks" consisting of hundreds or thousands of elements were still far out of reach. Initially, research was limited to individual units of neural networks, such as the perceptron or neuron. A key pioneer in this field was Frank Rosenblatt, who, during his time at the Cornell Aeronautical Laboratory from 1957 to 1959, developed a single perceptron consisting of 400 photosensitive units (inputs) connected via an "association layer" to an output layer of 8 units. Today, the Rosenblatt perceptron is considered the birth of neural networks and deep learning models.

Frank Rosenblatt (left) working on the Mark I Perceptron. Even decades later, in the 1980s, when neural networks experienced a resurgence of interest, their actual practical successes remained rather limited. Other algorithms, such as kernel methods (support vector machines) or decision trees, pushed neural networks to the back of the machine learning rankings in the 1980s and 1990s. At that time, neural networks had not yet been able to reach their full potential. On one hand, computing power was still insufficient, and on the other, more complex network architectures - like those used today - suffered from the so-called "vanishing gradient problem," which made training the networks even more difficult or entirely impossible. Until the early 2000s, the now-celebrated neural networks remained largely confined to the academic sidelines. It was not until 2006, when Geoffrey Hinton, one of the most renowned researchers in neural networks, published a groundbreaking paper demonstrating the successful training of a multilayer neural network for the first time, that the field regained attention in both research and practice. New methodological advancements, such as the specification of alternative activation functions designed to mitigate the vanishing gradient problem, as well as the development of distributed computing systems, fueled research and applications in neural networks. For more than a decade now, neural networks and deep learning have increasingly become synonymous with machine learning and artificial intelligence. They represent a booming scientific research field and are being applied in numerous practical scenarios. Deep learning models consistently outperform one another in solving complex machine learning tasks in speech and image recognition. Driven by rapid technological advancements in distributed computing and GPU computing, deep learning now appears to be in the right place at the right time to realize its full potential.

Neural Networks – A Reflection of the Brain?

Contrary to the widely held belief that neural networks are based on the functioning of the human brain, it can only be confirmed that modern deep learning models have, to some extent, been inspired by findings from neuroscience. Moreover, it is now well understood that the actual processes and functions involved in information processing in the brain are significantly more complex than what is represented in neural networks. However, the fundamental idea that many individual "computing units" (neurons) process information intelligently through interconnections can be acknowledged as a core principle. In the brain, neurons are connected via synapses, which can form or change between neurons. The figure below illustrates a pyramidal cell, one of the most common neuron structures in the human brain.

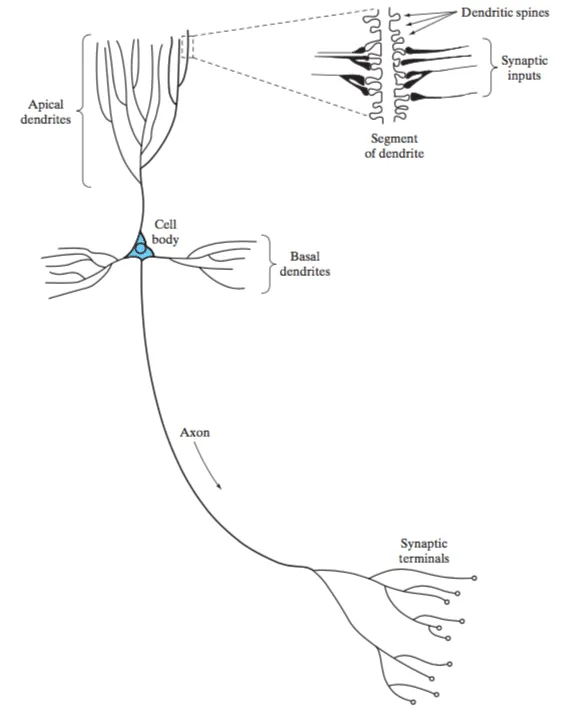
Like other types of neurons, the pyramidal cell receives most of its input signals through its dendrites, which, via the axon and its dendritic branches, can form tens of thousands or more connections to other neurons. According to the so-called convergence-divergence principle, the activation of individual neurons is influenced by many other cells, while at the same time, the neuron sends signals to many other cells. This creates a highly complex network of connections in the brain, used for information processing. Simply put, in the brain, individual neurons process the signals from other neurons (inputs) and transmit a new signal based on this to the next group of neurons. A single neuron is therefore represented by a specific biological (or mathematical) function that evaluates its input signals, generates an appropriate response signal, and transmits this within the network to further neurons. The term "network" arises from the fact that many of these neurons are grouped into layers, transmitting their signals to subsequent nodes or layers, thereby forming a network of interconnections between neurons.

What Is Deep Learning?

Deep learning today refers to neural network architectures that contain more than one hidden layer. The advantage of having multiple layers of neurons becomes evident in how "new" information is formed between the layers, representing abstractions of the original input data. It is crucial to understand that these representations are variations or abstractions of the initial input signals.

"Deep learning today refers to neural networks that contain more than one hidden layer."

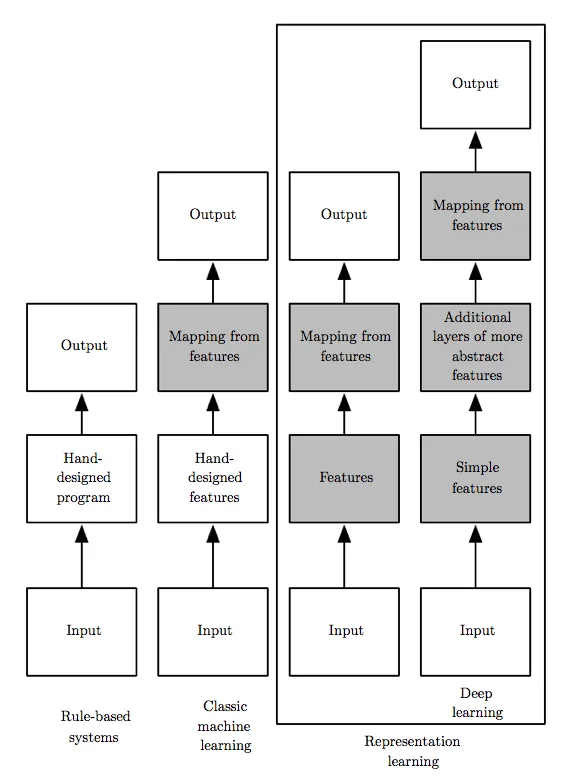
This mechanism, known as representation learning, enables deep learning models to generalize well to new data points. The reason for this is that the created abstractions of the data are significantly more general in nature than the original input data. Learning through representation is one of the key distinguishing features of deep learning compared to traditional machine learning models, which typically learn without explicit data representation. The following figure illustrates the difference between rule-based systems, traditional machine learning models, and deep learning.

Since deep learning models can theoretically contain a very large number of layers, their abstraction capacity is particularly high. This allows a deep learning model to form abstractions of input data at multiple levels and use them to solve machine learning problems. One example of such a complex architecture is GoogleNet, designed for image classification (see figure).

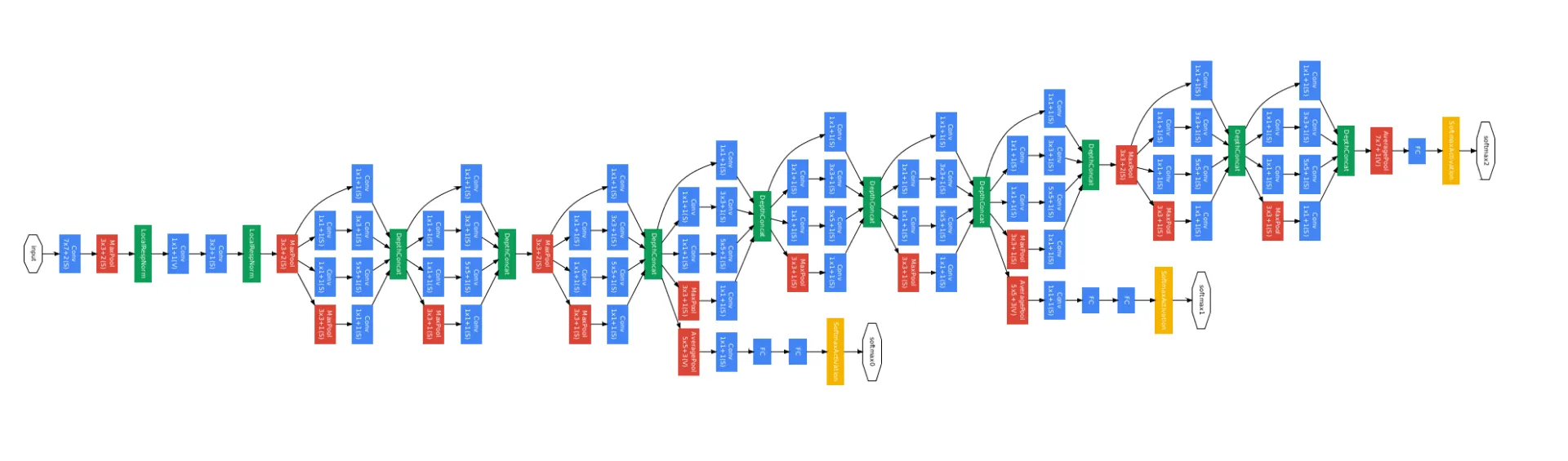
GoogleNet consists of multiple architectural blocks specifically designed for object and image recognition tasks. As a result, the network can recognize thousands of objects in images with high accuracy through representation learning.

Structure and Components of Neural Networks

Back to the basics. The fundamental building block of every neural network is the neuron. A neuron is a node in the neural network where one or more input signals (numerical data) converge and are processed by the neuron's activation function. The output of the neuron is thus a function of the input. There are various activation functions, which we will explore in more detail in later parts of our deep learning series. The elementary building block of any neural network is the neuron. A neuron is a node in the neural network where one or more input signals (inputs) come together and are processed. Depending on where the neuron is located in the network, these signals may originate either from the input layer or from preceding neurons. After processing the input signals, they are passed on as output to the subsequent neurons. Formally speaking, the output of a neuron is a function of the inputs. The following figure illustrates the basic structure:

‍

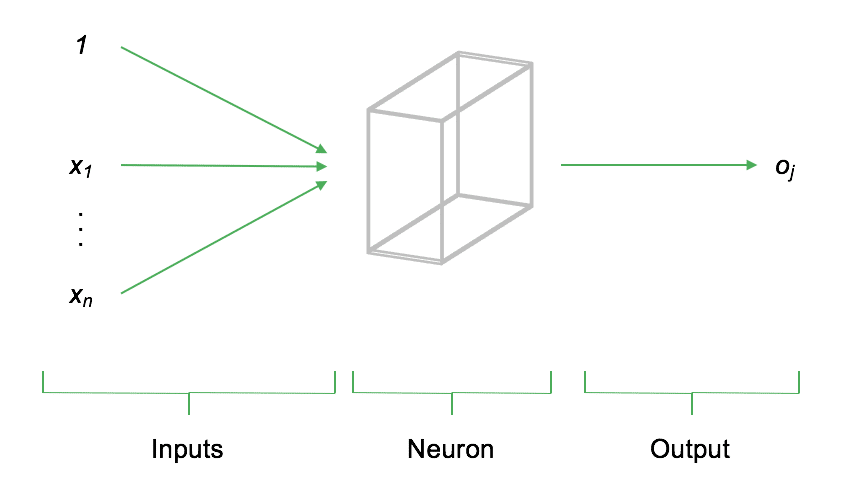
The figure above schematically represents the structure of a single neuron. On the left side of the diagram, the inputs §x_1,...,x_n$​ arrive at the neuron. Each input represents an arbitrary numerical value (e.g., existing data or signals from previous neurons). The neuron evaluates (weights) the input, computes the output $o_j$, and transmits it to the next connected neurons. The input of a neuron is therefore the weighted sum of all neurons connected to it from the previous layer. Typically, neural networks are not composed of single neurons but rather entire layers containing many of these nodes. These layers are called hidden layers and form the core of deep learning model architectures. In addition to the hidden layer, there is also an input layer and an output layer. The input layer serves as the entry point for data into the model, while the output layer represents the model's final result. In a simple architecture, all neurons in adjacent layers are fully connected. The following figure illustrates the structure of a basic neural network with an input layer, a hidden layer, and an output layer.

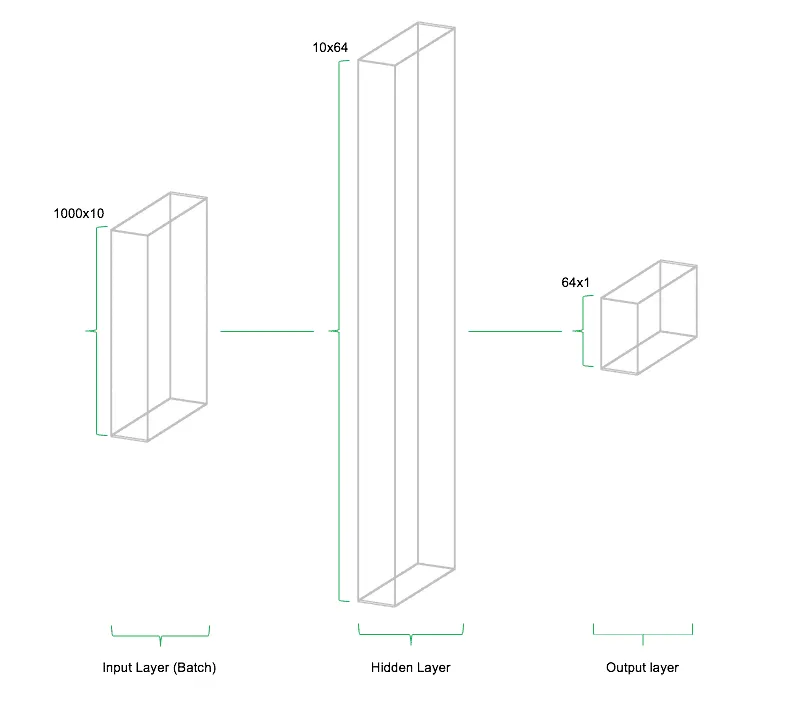
Die Verbindungen (Gewichte / Weights) zwischen den Neuronen sind derjenige Teil des neuronalen Netzes, der auf die vorliegenden Daten angepasst wird. Die Architektur des Netzes bleibt (zumindest in einfachen Architekturen) konstant während des Trainings. Die Gewichte werden von Iteration zu Iteration so angepasst, dass der Fehler, den das neuronale Netz während dem Trainings macht immer weiter reduziert wird. Während des Trainings werden Abweichungen der Schätzung des Netzwerks von den tatsächlich beobachteten Datenpunkten berechnet. Nach der Berechnung des Gesamtfehlers werden die Gewichte des Netzes rekursiv aktualisiert. Die Richtung dieser Aktualisierung wird so gewählt, dass der Fehler im nächsten Durchlauf kleiner wird. Diese Methodik nennt man "Gradient Descent" und beschreibt die iterative Anpassung der Modellparameter in entgegengesetzter Richtung zum Modellfehler. Auch heutzutage werden Deep Learning Modelle und neuronale Netze mittels Gradient Descent bzw. aktuelleren Abwandlungen davon trainiert.

Architekturen von neuronalen Netzen

Die Architektur von neuronalen Netzen kann durch den Anwender nahezu frei spezifiziert werden. Tools wie  TensorFlow  oder Theano ermöglichen es dem Anwender, Netzarchitekturen beliebiger Komplexität zu modellieren und auf den vorliegenden Daten zu schätzen. Zu den Parametern der Netzarchitektur zählen im einfachsten Falle die Anzahl der Hidden Layer, die Anzahl der Neuronen pro Layer sowie deren Aktivierungsfunktion. Im Rahmen der Forschung zu neuronalen Netzen und Deep Learning haben sich unterschiedlichste Architekturen von Netzwerken für spezifische Anwendungen entwickelt. Jede dieser Architekturen weist spezifische Vorteile und Eigenschaften auf, die die Verarbeitung von speziellen Informationen erleichtern sollen. So wird beispielsweise bei Convolutional Neural Networks (CNNs), die primär zur Verarbeitung von Bildinformationen eingesetzt werden, die räumliche Anordnung von Informationen berücksichtigt, bei Recurrent Neural Nets (RNNs) die zeitliche Anordnung von Datenpunkten. Im Folgenden sollen die wichtigsten Typen von Architekturen kurz skizziert werden.

Feedforward  Netze

Unter einem Feedforward  Netz versteht man ein neuronales Netz mit einer Inputschicht, einem oder mehreren Hidden Layers sowie einer Outputschicht. In der Regel handelt es sich bei den Hidden Layers um sogenannte "Dense Layers", d.h. voll vernetzte Neuronen mit Gewichtungen zu allen Neuronen der vorherigen und folgenden Schicht. Die folgende Abbildung zeigt ein Deep Learning Modell, das mit vier Hidden Layers konstruiert wurde.

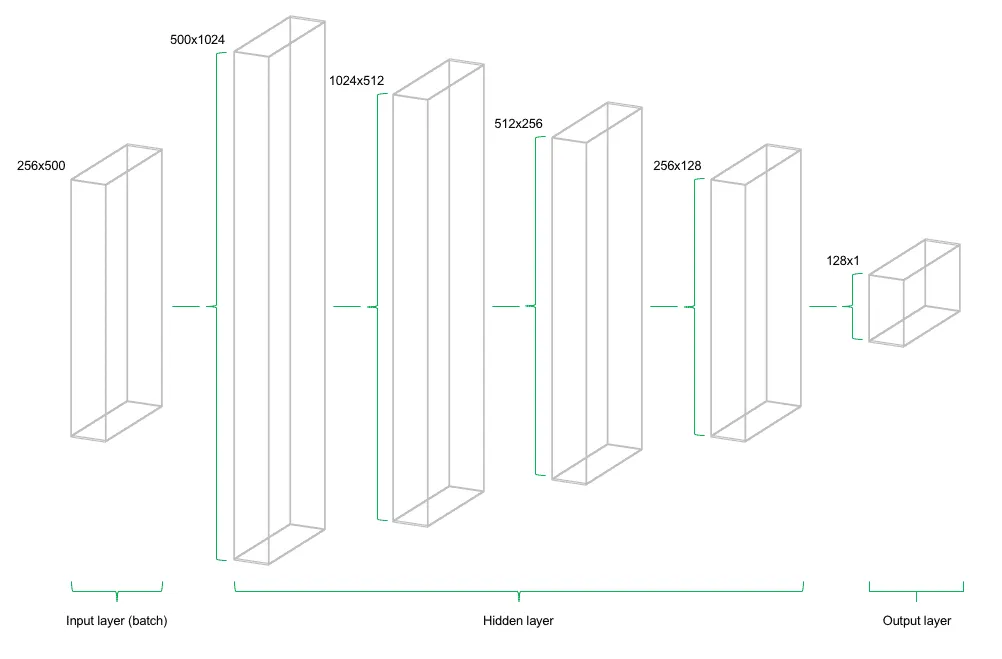
While multi-layer perceptrons (MLPs) serve as universal architectures for a wide range of problems, they exhibit certain weaknesses in specific application areas. For instance, in image classification, the number of neurons required increases exponentially with each additional pixel in the image, making MLPs inefficient for such tasks.

Convolutional Neural Networks (CNNs)

Convolutional neural networks (CNNs) are a specialized type of neural network designed for processing spatially structured data. This includes image data (2D), videos (3D), or audio signals (1D-2D). The architecture of CNNs differs significantly from that of a conventional feedforward network. CNNs are built using specialized layers known as convolutional layers and pooling layers. The purpose of these layers is to analyze the input from multiple perspectives. Each neuron in a convolutional layer examines a specific region of the input field using a filter, called a kernel. A filter detects specific features in the image, such as color composition or brightness. The result of applying a filter is a weighted transformation of a specific region, which is then stored in the convolutional layer.

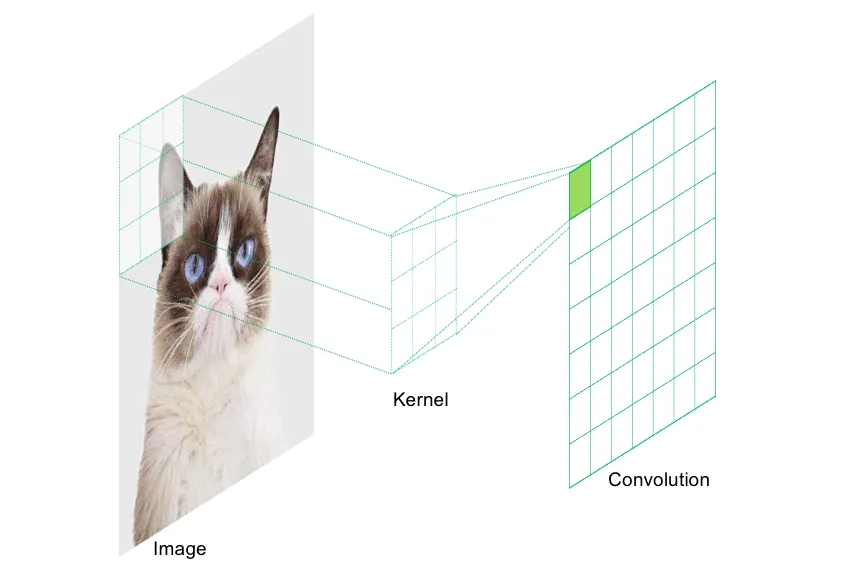
The size (or rather, depth) of a convolutional layer is determined by the number of filters, as each filter scans the entire input image. The information extracted by the filters is then compressed between convolutional layers using pooling layers. Pooling layers traverse the feature maps created by the filters and compress them by reducing the number of pixels based on a predefined logic. For example, they can apply max pooling (selecting the maximum value in a region) or average pooling (calculating the mean value). Additional convolutional and pooling layers can follow until the extracted features are passed into a fully connected MLP (multi-layer perceptron), which then processes the final estimates in the output layer. Convolutional and pooling layers effectively compress spatially structured information and reduce the number of weight parameters in the network. This makes it possible to process even high-dimensional images (e.g., high-resolution inputs) efficiently.

Recurrent Neural Networks (RNNs)

Recurrent neural networks (RNNs) represent a class of neural network architectures in which neurons pass their signals in a closed loop. This means that the output of a layer is fed back into the same layer as an input. As a result, the network can retain and incorporate information from observations that are temporally distant during training. This architectural approach makes RNNs particularly well-suited for analyzing sequential data, such as speech, text, or time-series data.

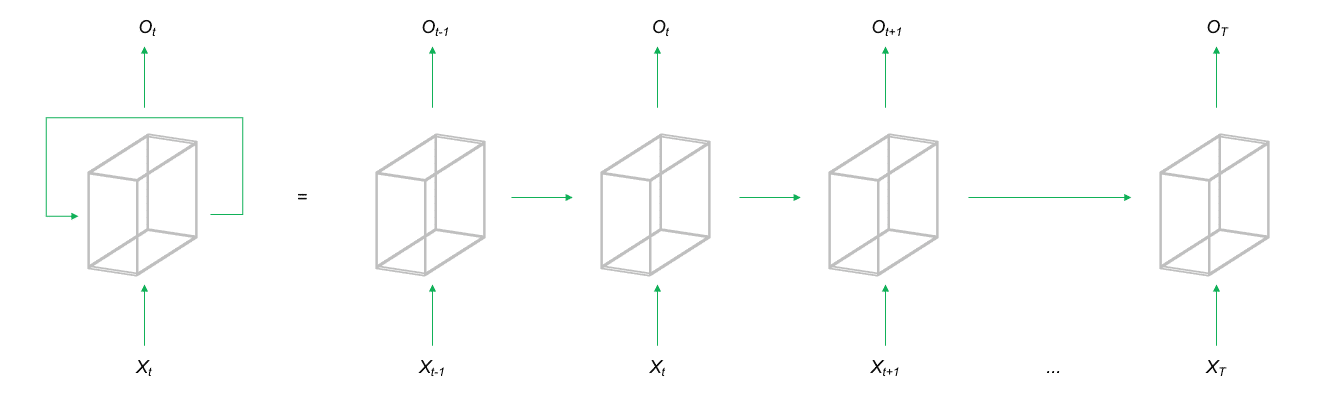
One of the most well-known RNN architectures is the Long Short-Term Memory (LSTM) network. In LSTMs, additional parameters are trained to store or discard input and output information for the next iteration, allowing the network to retain relevant information for predicting the next sequence segment. This enables the model to preserve previously encountered signals across the temporal dimension of the data and utilize them later. LSTMs are currently highly successful in Natural Language Processing (NLP), where they are used for text translation or training chatbots. Additionally, RNNs are well-suited for modeling sequences in general, such as time-series forecasting or Next Best Action recommendations.

Other Neural Network Architectures

Beyond the three main deep learning architectures discussed above, there are numerous variations and adaptations of CNNs and RNNs. One approach currently gaining significant attention in deep learning research is Generative Adversarial Networks (GANs). GANs are used to synthesize model inputs, generating new data points from the same probability distribution as the original inputs. This technique can be applied to create datasets, as well as generate image and audio content that matches the "style" of the original inputs. For example, GANs can be used to produce new texts that resemble the compositions of well-known writers or generate artwork inspired by the painting styles of famous artists.

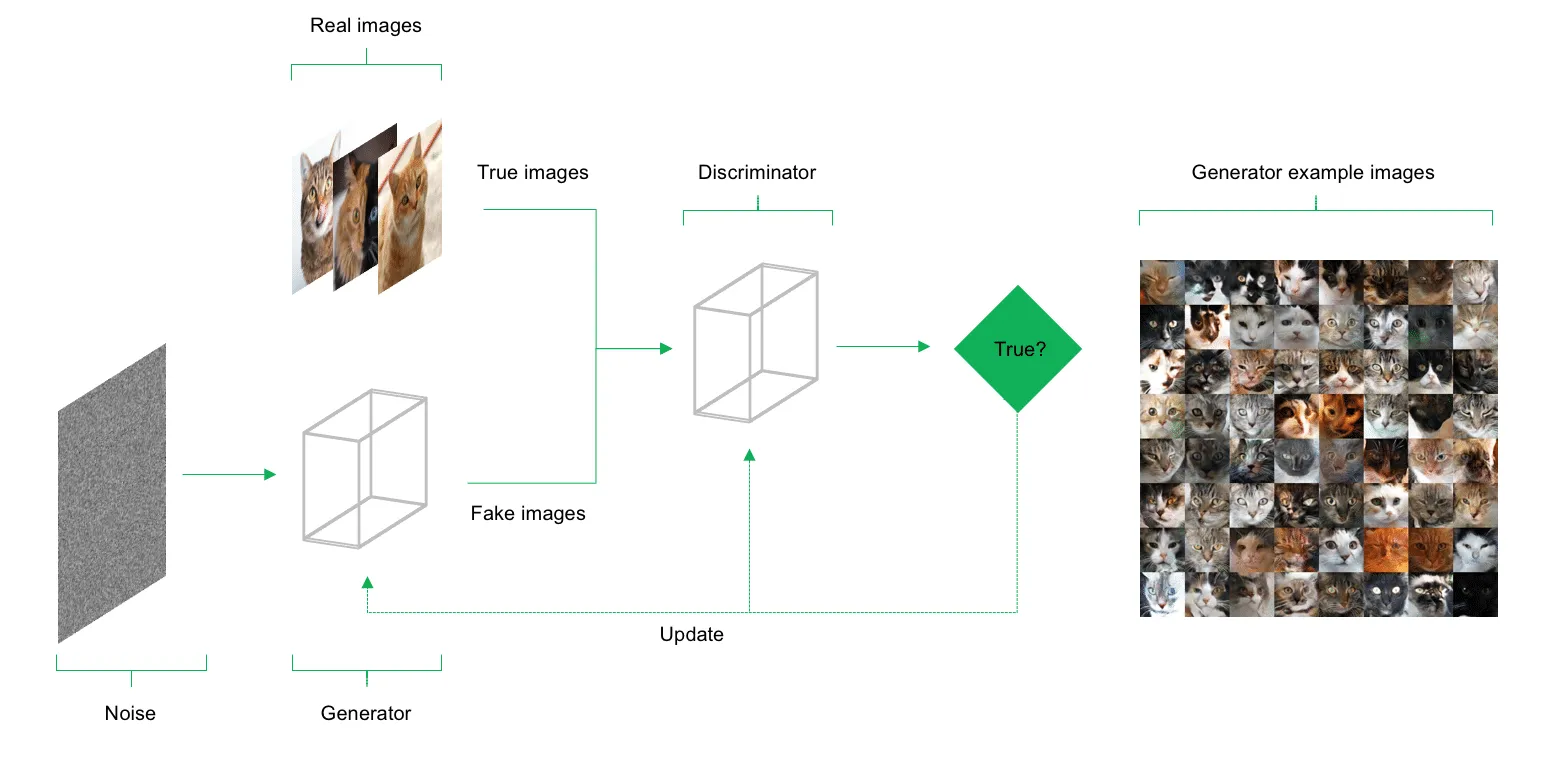
The application areas of GANs are extremely promising and forward-looking; however, training such networks remains experimental and is not yet fully understood. Nonetheless, initial models and results from current research are highly encouraging. Particularly exciting advancements are being made in the field of artificial image generation. Today, GANs are already being trained to simulate how a person might look in old age based on a single photo or to generate a 360-degree view of a subject from a frontal image. Another significant application of GANs is in text-to-image synthesis, where the model generates photorealistic images based on textual descriptions.

Summary and Outlook

Deep learning and neural networks are exciting machine learning methods applicable to a wide range of problems. Through representation learning—the ability to extract abstract concepts from data and use them to solve problems—deep learning models demonstrate high accuracy and generalizability for many complex tasks. The development of deep learning models, algorithms, and architectures is advancing rapidly, making it likely that deep learning will continue to establish itself as the benchmark in many machine learning disciplines. As technology continues to progress, increasingly complex architectures will become feasible. Even today, specialized deep learning hardware, such as Google's Tensor Processing Units (TPUs), is designed to meet the numerical demands of deep learning models, further accelerating advancements in the field.

References

1. Rosenblatt, Frank (1958). The perceptron. A probabilistic model for information storage and organization in the brain. Psychological Reviews, 65: S. 386–408.
2. Goodfellow, Ian; Bengio Yoshua; Courville, Cohan (2016). Deep Learning. MIT Press.
3. Haykin, Simon (2008). Neural Networks and Machine Learning. Pearson.
4. Bishop, Christopher M (1996). Neural Networks for Pattern Recognition. Oxford Press.