Data Science in Python – der Kern des Ganzen – Teil 2


Im vorherigen Teil dieser statworx Reihe haben wir uns mit verschiedenen Datenstrukturen auseinander gesetzt. Darunter jene, die uns in Python direkt 'Out of the box' zur Verfügung stehen, als auch NumPy's ndarrays. Bei den nativen Containern (z.B. Tuples oder Listen) konnten wir feststellen, dass nur die Listen unseren Anforderungen im Rahmen der Arbeit mit Daten - veränderbar und indizierbar - erfüllen. Jedoch waren diese relativ unflexibel und langsam, sobald wir versuchten, diese für rechenintensive mathematische Operationen zu nutzen. Zum einen mussten wir Operationen per Schleife auf die einzelnen Elemente anwenden und zum anderen waren Anwendungen aus der linearen Algebra, wie Matrizenmultiplikation nicht möglich. Daher wandten wir unsere Aufmerksamkeit den ndarrays von NumPy zu. Da NumPy den Kern der wissenschaftlichen Python-Umgebung darstellt, werden wir uns in diesem Teil genauer mit den Arrays befassen. Wir betrachten ihre Struktur tiefergehend und untersuchen woher die verbesserte Performance kommt. Abschließend werden wir darauf eingehen, wie man seine Analyse bzw. seine Ergebnisse speichern und erneut laden kann.
Attribute und Methoden
N-Dimensionen
Wie sämtliche Konstrukte in Python sind auch die ndarrays ein Objekt mit Methoden und Attributen. Das für uns interessanteste Attribut bzw. die interessanteste Eigenschaft ist, neben der Effizienz, die Multidimensionalität. Wie wir schon im letzten Teil gesehen haben, ist es einfach ein zweidimensionales Array zu erschaffen ohne dabei Objekte ineinander zu verschachteln, wie es bei Listen der Fall wäre. Stattdessen können wir einfach angeben, wie groß das jeweilige Objekt sein soll, wobei eine beliebige Dimensionalität gewählt werden kann. Typischerweise wird dies über das Argument ndim angegeben. NumPy bietet uns zusätzlich die Möglichkeit beliebig große Arrays außerordentlich simpel umzustrukturieren. Die Umstrukturierung der Dimensionalität eines ndarray erfolgt dabei durch die reshape()-Methode. Ihr wird ein Tupel oder eine Liste mit der entsprechenden Größe übergeben. Um ein umstrukturiertes Array zu erhalten, muss die Anzahl der Elemente mit der angegebenen Größe kompatibel sein.
# 2D-Liste
list_2d = [[1,2], [3,4]]
# 2D-Array
array_2d = np.array([1,2,3,4]).reshape((2,2))
# 10D-Array
array_10d = np.array(range(10), ndmin=10)
Um an strukturelle Informationen eines Arrays wie zum Beispiel der Dimensionalität zu gelangen, können wir die Attributendim, shape oder size aufrufen. So bietet uns beispielsweise ndim Aufschluss über die Anzahl der Dimensionen, während uns size verrät, wie viele Elemente sich in dem jeweiligen Array befinden. Das Attribut shape verbindet diese Informationen und gibt an, wie die jeweiligen Einträge auf die Dimensionen aufgeteilt sind.
# Erstellung eines 3x3x3 Arrays mit den Zahlen 0 bis 26
Arr = np.arange(3*3*3).reshape(3,3,3)
# Anzahl der Dimension
Arr.ndim # =3
# Anzahl der Elemente , 27
Arr.size # =27
# Detaillierte Aufgliederung dieser beiden Informationen
Arr.shape # = (3,3,3) Drei Elemente pro Dimension
Indizierung
Nach dem wir nun herausfinden können wie unser ndarray aufgebaut ist, stellt sich die Frage, wie wir die einzelnen Elemente oder Bereiche eines Arrays auswählen können. Diese Indizierung beziehungsweise das Slicing erfolgt dabei prinzipiell wie bei Listen. Durch die []-Notation können wir auch bei den Arrays einen einzelnen Index oder per :-Syntax ganze Folgen abrufen. Die Indizierung per Index ist relativ simpel. Zum Beispiel erhalten wir den ersten Wert des Arrays durch Arr[0] und durch ein vorangestelltes - erhalten wir den letzten Wert des Arrays durch Arr[-1]. Wollen wir jedoch eine Sequenz von Daten abrufen, können wir die :-Syntax nutzen. Diese folgt dem Schema [ Start : Ende : Schritt ], wobei sämtliche Argumente optional sind. Dabei ist anzumerken, dass nur die Daten exklusiv des angegebenen Ende ausgegeben werden. Somit erhalten wir durch Arr[0:2] nur die ersten beiden Einträge. Die Thematik wird in der folgenden Grafik verdeutlicht.
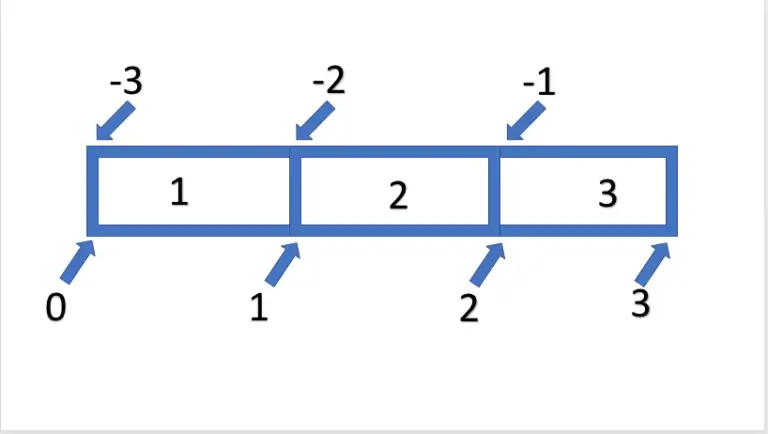
Wollen wir das gesamte Array mit dieser Logik auswählen, kann man auch den Start und / oder das Ende weglassen wodurch es automatisch ergänzt wird. So könnten wir mit Arr[:2] vom Ersten bis zum zweiten Element oder mit Arr[1:] vom Zweiten bis zum Letzten Element selektieren.
Als nächstes wollen wir auf das bisher ausgelassene Argument Schritt eingehen. Dies erlaubt es uns die Schrittweite, zwischen dem Element, zwischen Start und Ende festzulegen. Wollen wir beispielsweise nur jedes zweite Element des gesamten Arrays können wir den Start und das Ende weglassen und nur eine Schrittweite von 2 definieren - Arr[::2]. Wie bei der umgedrehten Indizierung, ist auch eine umgedrehte Schrittweite durch negative Werte möglich. Demnach führt eine Schrittweite von -1 dazu, dass das Array in umgedrehter Reihenfolge ausgegeben wird.
arrarr = np.array([1,1,2,2,3,3])
arr = np.array([1,2,3])
arrarr[::2] == arr
rra = np.array([3,2,1])
arr[::-1] == rra & rra[::-1] ==arr
TrueSofern wir diesen nun auf ein Array übertragen wollen, welches nicht im eindimensionalen Raum, sondern in einem mehrdimensionalen Raum vorliegt, können wir einfach jede weitere Dimension als eine weitere Achse betrachten. Demzufolge können wir auch das Slicen eines eindimensionalen Arrays relativ leicht auf höhere Dimensionen übertragen. Hierfür müssen wir nur jede Dimension einzeln zerteilen und die einzelnen Befehle nur per Kommata trennen. Um so anhand dieser Syntax eine gesamte Matrix der Größe 3x3 zu selektieren, müssen wir also die gesamte erste und zweite Achse auswählen. Analog zu vorher würden wir also zweimal [:] benutzen. Dieses würden wir nun in einer Klammer formulieren als [:,:]. Dieses Schema lässt sich für beliebig viele Achsen erweitern. Hier ein paar weitere Beispiele:
arr = np.arange(8).reshape((2,2,2))
#das ganze Array
arr[:,:,:]
# Jeweils das erste Element
arr[0,0,0]
# Jeweils das letzte Element
arr[-1,-1,-1]Rechnen mit Arrays
UFuncs
Wie schon des Öfteren innerhalb dieses und des letzten Beitrages erwähnt, liegt die große Stärke von NumPy darin, dass das Rechnen mit ndarray äußerst performant ist. Der Grund dafür liegt zunächst an den Arrays die ein effizienter Speicher sind und es ermöglichen höherdimensionale Räume mathematisch abzubilden. Der große Vorteil von NumPy liegt dabei jedoch vor allem an den Funktionen die wir zur Verfügung gestellt bekommen. So ist es erst durch die Funktionen möglich, nicht mehr über die einzelnen Elemente per Schleife zu iterieren, sondern das gesamte Objekt übergeben zu können und auch nur eins wieder herauszubekommen. Diese Funktionen werden 'UFuncs' genannt und zeichnen sich dadurch aus, dass sie so konstruiert und kompiliert sind, um auf einem gesamten Array zu arbeiten. Sämtliche Funktionen, die uns durch NumPy zugänglich sind, besitzen diese Eigenschaften, so auch die np.sqrt-Funktion, die wir im letzten Teil genutzt haben. Hinzu kommen auch noch die speziellen - extra für Arrays - definierten mathematischen Operatoren, wie +, -, *…. Da auch diese letztendlich nur Methoden eines Objektes sind (z.B. ist a.__add__(b) das Gleiche wie a + b), wurden die Operatoren für NumPy Objekte als Ufunc-Methoden implementiert, um eine effiziente Kalkulation zu gewährleisten.Die entsprechenden Funktionen könnten wir auch direkt ansprechen:
Dynamische Dimensionen via Broadcasting
Ein weiterer Vorteil von Arrays besteht außerdem darin, dass eine dynamische Anpassung der Dimensionen durch Broadcasting stattfindet, sobald eine mathematische Operation ausgeführt wird. Wollen wir also einen 3x1 Vektor und eine 3x3 Matrix elementweise miteinander multiplizieren, wäre dieses in der Algebra nicht trivial zu lösen. NumPy 'streckt' daher den Vektor zu einer weiteren 3x3 Matrix und führt dann die Multiplikation aus.
Dabei erfolgt die Anpassung über drei Regeln:
- Regel 1: Wenn sich zwei Arrays in der Anzahl der Dimensionen unterscheiden, wird das kleine Array angepasst mit zusätzlichen Dimensionen auf der linken Seite, z.B. (3,2) -> (1,3,2)
- Regel 2: Sofern sich die Arrays in keiner Dimension gleichen, wird das Array mit einer unären Dimension gestreckt, wie es im oberen Beispiel der Fall war (3x1) -> 3x*3
- Regel 3: Sofern weder Regel 1 noch Regel 2 greifen, wird ein Fehler erzeugt.
# Regel 1
arr_1 = np.arange(6).reshape((3,2))
arr_2 = np.arange(6).reshape((1,3,2))
arr_2*arr_1 # ndim = 1,3,2
# Regel 2
arr_1 = np.arange(6).reshape((3,2))
arr_2 = np.arange(2).reshape((2))
arr_2*arr_1 # ndim = 3,2
# Regel 3
arr_1 = np.arange(6).reshape((3,2))
arr_2 = np.arange(6).reshape((3,2,1))
arr_2*arr_1 # Error, da rechts aufgefüllt werden müsste und nicht links ValueErrorTraceback (most recent call last)
<ipython-input-4-d4f0238d53fd> in <module>()
12 arr_1 = np.arange(6).reshape((3,2))
13 arr_2 = np.arange(6).reshape((3,2,1))
---> 14 arr_2*arr_1 # Error da rechts aufgefüllt werden müsste und nicht links
ValueError: operands could not be broadcast together with shapes (3,2,1) (3,2)An diesem Punkt sollte man noch anmerken, dass Broadcasting nur für elementweise Operationen gilt. Sofern wir uns der Matrizenmultiplikation bedienen, müssen wir selber dafür sorgen, dass unsere Dimensionen stimmen. Wollen wir bNueispielhaft eine 3x1 Matrix mit einem Array der Größe 3 multiplizieren, wird nicht wie in Regel 2 die kleine Matrix links erweitert, sondern direkt ein Fehler erzeugt.
arr_1 = np.arange(3).reshape((3,1))
arr_2 = np.arange(3).reshape((3))
# Fehler
arr_1@arr_2ValueErrorTraceback (most recent call last)
<ipython-input-5-8f2e35257d22> in <module>()
3
4 # Fehler
----> 5 arr_1@arr_2
ValueError: shapes (3,1) and (3,) not aligned: 1 (dim 1) != 3 (dim 0)
Bekannter und verständlicher als diese dynamische Anpassung sollten Aggregation als Beispiel für Broadcasting sein.
Neben den direkten Funktionen für die Summe oder den Mittelwert, lassen sich diese nämlich auch über die Operatoren abbilden. So kann man die Summe eines Array nicht nur per np.sum(x, axis=None) erhalten, sondern auch über np.add.reduce(x, axis = None ). Diese Form des Operatoren-Broadcasting erlaubt es uns auch die jeweilige Operation akkumuliert anzuwenden, um so rollierende Werte herauszubekommen. Über die Angabe der axis können wir bestimmen, entlang welcher Achse die Operation ausgeführt werden soll. Im Fall von np.sum oder np.mean ist None der Standard. Dies bedeutet, dass sämtliche Achsen einbezogen werden und ein Skalar entsteht. Sofern wir das Array jedoch nur um eine Achse reduzieren möchten, können wir den jeweiligen Index der Achse angeben:
# Reduziere alle Achsen
np.add.reduce(arr_1, axis=None)
# Reduzieren der dritten Achse
np.add.reduce(arr, axis=2)
# Kummulierte Summe
np.add.accumulate(arr_1)
# Kummmuliertes Produkt
np.multiply.accumulate(arr_1)
Speichern und Laden von Daten
Als letztes wollen wir nun auch noch in der Lage sein unsere Ergebnisse zu speichern und beim nächsten Mal zu laden. Hierbei stehen uns in NumPy generell zwei Möglichkeiten offen. Nummer 1 ist die Verwendung von textbasierten Formaten wie z.B. .csv durch savetxt und loadtxt. Werfen wir nun einen Blick auf die wichtigsten Eigenschaften dieser Funktionen, wobei der Vollständigkeit halber sämtliche Argumente aufgelistet werden, jedoch nur Bezug auf die wichtigsten genommen wird.
Das Speichern von Daten erfolgt dem Namen entsprechend durch die Funktion:
np.savetxt(fname, X, fmt='%.18e', delimiter=' ', newline='n', header='', footer='', comments='# ', encoding=None)
Über diesen Befehl können wir ein Objekt X in einer Datei fname speichern. Hierbei ist es prinzipiell egal, in welchem Format wir es speichern wollen, da das Objekt in Klartext gespeichert wird. Somit spielt es keine Rolle, ob wir als Suffix txt oder csv anfügen, die Namen entsprechen dabei nur Konventionen. Welche Werte zur Separierung genutzt werden sollen, geben wir durch die Schlüsselworte delimeter und newline an, welche im Fall eines csv ein ',' zur Separierung der einzelnen Werte / Spalten und ein n für eine neue Reihe sind. Per header und footer können wir optional angeben, ob wir weitere (String) Informationen an den Anfang oder das Ende der Datei schreiben wollen. Durch die Angabe von fmt - was für Format steht - können wir beeinflussen, ob und wie die einzelnen Werte formatiert werden sollen, also ob, wie und wie viele Stellen vor und nach dem Komma angezeigt werden sollen. Hierdurch können wir die Zahlen z.B. besser lesbar machen oder den Bedarf an Speicher auf der Festplatte verringern in dem wir die Präzision senken. Ein simples Beispiel wäre fmt = %.2 würde sämtliche Zahlen auf die zweite Nachkommastelle Runden ( 2.234 -> 2.23).
Das Laden der vorher gespeicherten Daten erfolgt durch die Funktion loadxt, die viele Argumente besitzt, die mit den Funktionen zum Speichern der Objekte übereinstimmt.
np.loadtxt(fname, dtype=<class 'float'>, comments='#', delimiter=None, converters=None, skiprows=0, usecols=None, unpack=False, ndmin=0, encoding='bytes')
Die Argumente fname und delimiter besitzen die selbe Funktionalität und Standardwerte wie beim Speichern der Daten. Durch skiprows kann angegeben werden, ob und wie viele Zeilen übersprungen werden sollen und durch usecols wird mit einer Liste von Indizes bestimmt, welche Spalten eingelesen werden sollen.
# Erstelle ein Bespiel
x = np.arange(100).reshape(10,10)
# Speicher es als CSV
np.savetxt('example.txt',x)
# Erneutes Laden
x = np.loadtxt(fname='example.txt')
# Überspringen der ersten fünf Zeilen
x = np.loadtxt(fname='example.txt', skiprows=5)
# Lade nur die erste und letzte Spalte
x = np.loadtxt(fname='example.txt', usecols= (0,-1))
Die zweite Möglichkeit Daten zu speichern sind binäre .npy Dateien. Hierdurch werden die Daten komprimiert, wodurch Sie zwar weniger Speicherplatz benötigen, jedoch auch nicht mehr direkt lesbar sind wie zum Beispiel txt oder csv Dateien. Darüber hinaus sind auch die Möglichkeiten beim Laden und Speichern vergleichsweise limitiert.
np.save(file, arr, allow_pickle=True, fix_imports=True)np.load(file, mmap_mode=None, allow_pickle=True, fix_imports=True, encoding='ASCII')
Für uns sind lediglich file und arr interessant. Wie der Name wahrscheinlich vermuten lässt, können wir durch das Argument file wieder angeben, in welcher Datei unser Array arr gespeichert werden soll. Analog dazu können wir auch beim Laden per load die zu ladende Datei über file bestimmen.
# Komprimieren und Speichern
np.save('example.npy', x )
# Laden der komprimierten Datei
x = np.load('example.npy')
Vorschau
Da wir uns nun mit dem mathematischen Kern der Data Science Umgebung vertraut gemacht haben, können wir uns im nächsten Teil damit beschäftigen, unseren Daten etwas mehr inhaltliche Struktur zu verpassen. Hierfür werden wir die nächste große Bibliothek erkunden - nämlich Pandas. Dabei werden uns mit den zwei Hauptobjekten - Series und DataFrame - der Bibliothek bekannt machen durch die wir wir bestehende Datensätze nutzen und diese direkt modifizieren und manipulieren können.


