Statistics & Methods Archives

Die versteckten Risiken von Black-Box Algorithmen

Unzählige Lebensläufe in kürzester Zeit sichten, bewerten und Empfehlungen für geeignete Kandidat:innen abgeben – das ist mit künstlicher Intelligenz im Bewerbungsmanagement mittlerweile möglich. Denn fortschrittliche KI-Techniken können auch komplexe Datenmengen effizient analysieren. Im Personalmanagement kann so nicht nur wertvolle Zeit bei der Vorauswahl eingespart, sondern auch Bewerber:innen schneller kontaktiert werden. Künstliche Intelligenz hat auch das Potenzial, Bewerbungsprozesse fairer und gerechter zu gestalten.

Die Praxis zeigt jedoch, dass auch künstliche Intelligenzen nicht immer „fairer“ sind. Vor einigen Jahren sorgte beispielsweise ein Recruiting-Algorithmus von Amazon für Aufsehen. Die KI diskriminierte Frauen bei der Auswahl von Kandidat:innen. Und auch bei Algorithmen zur Gesichtserkennung von People of Color kommt es immer wieder zu Diskriminierungsvorfällen.

Ein Grund dafür ist, dass komplexe KI-Algorithmen auf Basis der eingespeisten Daten selbstständig Vorhersagen und Ergebnisse berechnen. Wie genau sie zu einem bestimmten Ergebnis kommen, ist zunächst nicht nachvollziehbar. Daher werden sie auch als Black-Box Algorithmen bezeichnet. Im Fall von Amazon hat dieser auf Basis der aktuellen Belegschaft, die vorwiegend männlich war, geeignete Bewerber:innenprofile ermittelt und damit voreingenommene Entscheidungen getroffen. Auf diese oder ähnliche Weise können Algorithmen Stereotypen reproduzieren und Diskriminierung verstärken.

Prinzipien für vertrauenswürdige KI

Der Amazon-Vorfall zeigt, dass Transparenz bei der Entwicklung von KI-Lösungen von hoher Relevanz ist, um die ethisch einwandfreie Funktionsweise sicherzustellen. Deshalb ist Transparenz auch eines der insgesamt sieben statworx Principles für vertrauenswürdige KI. Die Mitarbeitenden von statworx haben gemeinsam folgende KI-Prinzipien definiert: Menschen-zentriert, transparent, ökologisch, respektvoll, fair, kollaborativ und inklusiv. Diese dienen als Orientierung für die alltägliche Arbeit mit künstlicher Intelligenz. Allgemeingültige Standards, Regeln und Gesetzte gibt es nämlich bisher nicht. Dies könnte sich jedoch bald ändern.

Die europäische Union (EU) diskutiert seit geraumer Zeit einen Gesetzesentwurf zur Regulierung von künstlicher Intelligenz. Dieser Entwurf, der so genannte AI-Act, hat das Potenzial zum Gamechanger für die globale KI-Branche zu werden. Denn nicht nur europäische Unternehmen werden von diesem Gesetzesentwurf anvisiert. Betroffen wären alle Unternehmen, die KI-Systeme auf dem europäischen Markt anbieten, dessen KI-generierter Output innerhalb der EU genutzt wird oder KI-Systeme zur internen Nutzung innerhalb der EU betreiben. Die Anforderungen, die ein KI-System dann erfüllen muss, hängen von dessen Anwendungsbereich ab.

Recruiting-Algorithmen werden auf Grund ihres Einsatzbereichs voraussichtlich als Hochrisiko-KI eingestuft. Demnach müssten Unternehmen bei der Entwicklung, der Veröffentlichung aber auch beim Betrieb der KI-Lösung umfassende Auflagen erfüllen. Unter anderem sind Unternehmen in der Pflicht, Qualitätsstandards für genutzte Daten einzuhalten, technische Dokumentationen zu erstellen und Risikomanagement zu etablieren. Bei Verstoß drohen hohe Bußgelder bis zu 6% des globalen jährlichen Umsatzes. Daher sollten sich Unternehmen schon jetzt mit den kommenden Anforderungen und ihren KI-Algorithmen auseinandersetzen. Ein sinnvoller erster Schritt können Explainable AI Methoden (XAI) sein. Mit Hilfe dieser können Black-Box-Algorithmen nachvollzogen und die Transparenz der KI-Lösung erhöht werden.

Die Black-Box mit Explainable AI Methoden entschlüsseln

Durch XAI-Methoden können Entwickler:innen die konkreten Entscheidungsprozesse von Algorithmen besser interpretieren. Das heißt, es wird transparent, wie ein Algorithmus Muster und Regeln gebildet hat und Entscheidungen trifft. Dadurch können mögliche Probleme wie beispielsweise Diskriminierung im Bewerbungsprozess nicht nur entdeckt, sondern auch korrigiert werden. Somit trägt XAI nicht nur zur stärkeren Transparenz von KI bei, sondern begünstigt auch deren ethisch unbedenklichen Einsatz und fördert so die Konformität einer KI mit dem kommenden AI-Act.

Einige XAI-Methoden sind sogar modellagnostisch, also anwendbar auf beliebige KI-Algorithmen vom Entscheidungsbaum bis hin zum Neuronalen Netz. Das Forschungsfeld rund um XAI ist in den letzten Jahren stark gewachsen, weshalb es mittlerweile eine große Methodenvielfalt gibt. Dabei zeigt unsere Erfahrung aber: Es gibt große Unterschiede zwischen verschiedenen Methoden hinsichtlich Verlässlichkeit und Aussagekraft ihrer Ergebnisse. Außerdem eignen sich nicht alle Methoden gleichermaßen zur robusten Anwendung in der Praxis und zur Gewinnung des Vertrauens externer Stakeholder. Daher haben wir unsere Top 3 Methoden anhand der folgenden Kriterien für diesen Blogbeitrag ermittelt:

Ist die Methode modellagnostisch, funktioniert sie also für alle Arten von KI-Modellen?
Liefert die Methode globale Ergebnisse, sagt also etwas über das Modell als Ganzes aus?
Wie aussagekräftig sind die resultierenden Erklärungen?
Wie gut ist das theoretische Fundament der Methode?
Können böswillige Akteure die Resultate manipulieren oder sind sie vertrauenswürdig?

Unsere Top 3 XAI Methoden im Überblick

Anhand der oben genannten Kriterien haben wir drei verbreitete und bewährte Methoden zur detaillierten Darstellung ausgewählt: Permutation Feature Importance (PFI), SHAP Feature Importance und Accumulated Local Effects (ALE). Im Folgenden erklären wir für jede der drei Methoden den Anwendungszweck und deren grundlegende technische Funktionsweise. Außerdem gehen wir auf die Vor- und Nachteile beim Einsatz der drei Methoden ein und illustrieren die Anwendung anhand des Beispiels einer Recruiting-KI.

Mit Permutation Feature Importance effizient Einflussfaktoren identifizieren

Ziel der Permutation Feature Importance (PFI) ist es, herauszufinden, welche Variablen im Datensatz besonders entscheidend dafür sind, dass das Modell genaue Vorhersagen trifft. Im Falle des Recruiting-Beispiels kann die PFI-Analyse darüber aufklären, auf welche Informationen sich das Modell für seine Entscheidung besonders verlässt. Taucht hier z.B. das Geschlecht als einflussreicher Faktor auf, kann das die Entwickler:innen alarmieren. Aber auch in der Außenwirkung schafft die PFI-Analyse Transparenz und zeigt externen Anwender:innen an, welche Variablen für das Modell besonders relevant sind. Für die Berechnung der PFI benötigt man zunächst zwei Dinge:

Eine Genauigkeitsmetrik wie z.B. die Fehlerrate (Anteil falscher Vorhersagen an allen Vorhersagen)
Einen Testdatensatz, der zur Ermittlung der Genauigkeit verwendet werden kann.

Im Testdatensatz wird zunächst eine Variable nach der anderen durch das Hinzufügen von zufälligem Rauschen („Noise“) gewissermaßen verschleiert und dann die Genauigkeit des Modells über den bearbeiteten Testdatensatz bestimmt. Nun ist naheliegend, dass die Variablen, deren Verschleierung die Modellgenauigkeit am stärksten beeinträchtigen, besonders wichtig für die Genauigkeit des Modells sind. Sind alle Variablen nacheinander analysiert und sortiert, erhält man eine Visualisierung wie die in Abbildung 1. Anhand unseres künstlich erzeugten Beispieldatensatzes lässt sich folgendes erkennen: Berufserfahrung spielte keine große Rolle für das Modell, die Eindrücke aus dem Vorstellungsgespräch hingegen schon.

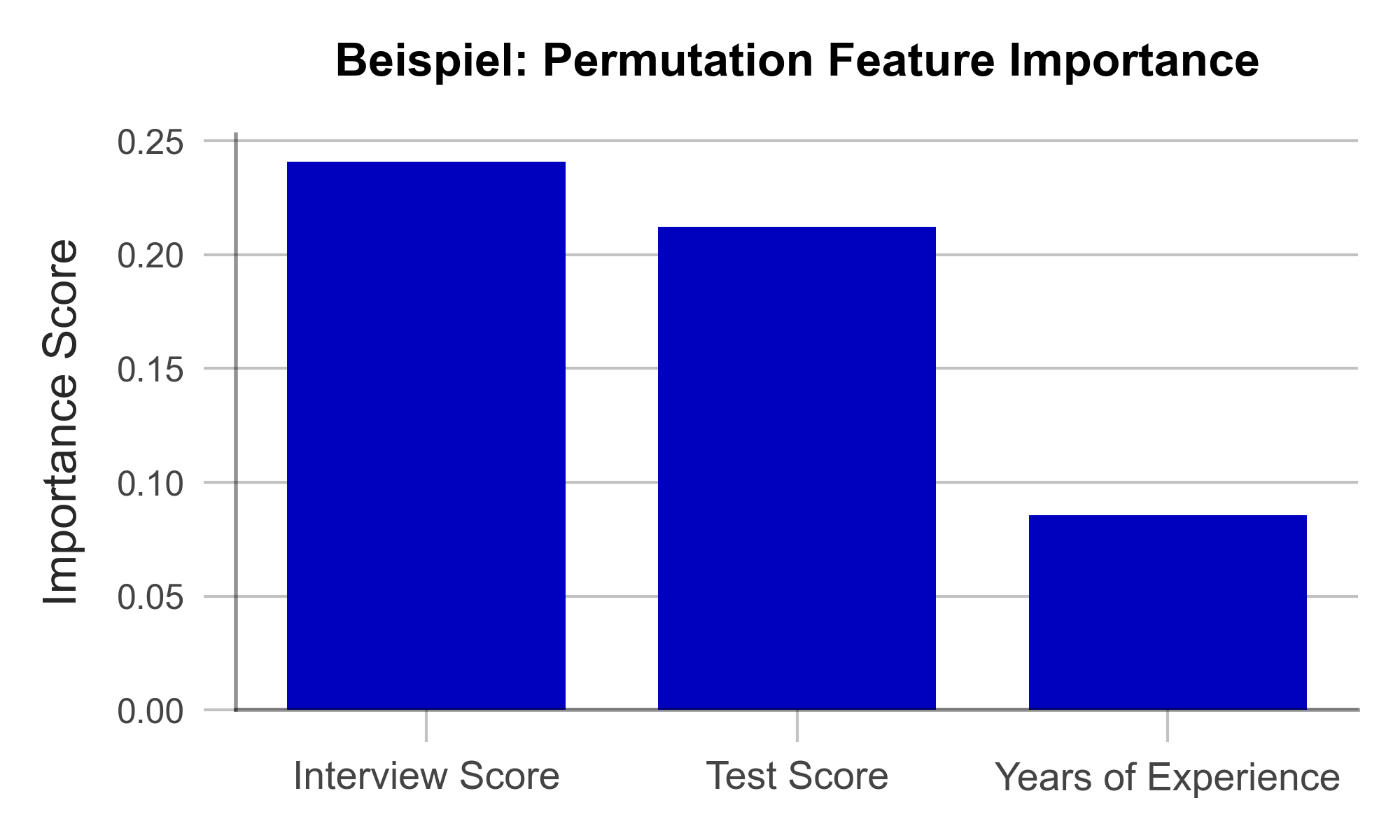
Abbildung 1 – Permutation Feature Importance am Beispiel einer Recruiting-KI (Daten künstlich erzeugt).

Eine große Stärke der PFI ist, dass sie einer nachvollziehbaren mathematischen Logik folgt. Die Korrektheit der gelieferten Erklärung kann durch statistische Überlegungen nachgewiesen werden. Darüber hinaus gibt es kaum manipulierbare Parameter im Algorithmus, mit der die Ergebnisse bewusst verzerrt werden könnten. Damit ist die PFI besonders geeignet dafür, das Vertrauen externer Betrachter:innen zu gewinnen. Nicht zuletzt ist die Berechnung der PFI im Vergleich zu anderen Explainable AI Methoden sehr ressourcenschonend.

Eine Schwäche der PFI ist, dass sie unter gewissen Umständen missverständliche Erklärungen liefern kann. Wird einer Variable ein geringer PFI-Wert zugewiesen, heißt das nicht immer, dass die Variable unwichtig für den Sachverhalt ist. Hat z.B. die Note des Bachelorstudiums einen geringen PFI-Wert, so kann das lediglich daran liegen, dass das Modell stattdessen auch die Note des Masterstudiums betrachten kann, da diese oft ähnlich sind. Solche korrelierten Variablen können die Interpretation der Ergebnisse erschweren. Nichtsdestotrotz ist die PFI eine effiziente und nützliche Methode zur Schaffung von Transparenz in Black-Box Modellen.

Stärken	Schwächen
Wenig Spielraum für Manipulation der Ergebnisse	Berücksichtigt keine Interaktionen zwischen Variablen
Effiziente Berechnung

Mit SHAP Feature Importance komplexe Zusammenhänge aufdecken

Die SHAP Feature Importance ist eine Methode zur Erklärung von Black-Box-Modellen, die auf der Spieltheorie basiert. Ziel ist es, den Beitrag jeder Variable zur Vorhersage des Modells zu quantifizieren. Damit ähnelt sie der Permutation Feature Importance auf den ersten Blick stark. Im Gegensatz zur PFI liefert die SHAP Feature Importance aber Ergebnisse, die komplexe Zusammenhänge zwischen mehreren Variablen berücksichtigen können.

SHAP liegt ein Konzept aus der Spieltheorie zugrunde: die Shapley Values. Diese sind ein Fairness-Kriterium, das jeder Variable eine Gewichtung zuweist, die ihrem Beitrag zum Ergebnis entspricht. Naheliegend ist die Analogie zu einem Teamsport, bei dem das Siegerpreisgeld unter allen Spieler:innen fair, also gemäß deren Beitrag zum Sieg, aufgeteilt wird. Mit SHAP kann analog für jede einzelne Beobachtung im Datensatz analysiert werden, welchen Beitrag welche Variable zur Vorhersage des Modells geliefert hat

Ermittelt man nun den durchschnittlichen absoluten Beitrag einer Variable über alle Beobachtungen im Datensatz hinweg, erhält man die SHAP Feature Importance. Abbildung 2 veranschaulicht beispielhaft die Ergebnisse dieser Analyse. Die Ähnlichkeit zur PFI ist klar ersichtlich, auch wenn die SHAP Feature Importance die Bewertung des Vorstellungsgespräches nur auf Platz 2 setzt.

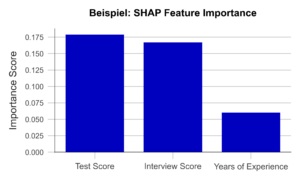
Abbildung 2 – SHAP Feature Importance am Beispiel einer Recruiting KI (Daten künstlich erzeugt).

Ein großer Vorteil dieses Ansatzes ist die Möglichkeit, Interaktionen zwischen Variablen zu berücksichtigen. Durch die Simulation verschiedener Variablen-Kombinationen lässt sich zeigen, wie sich die Vorhersage ändert, wenn zwei oder mehr Variablen gemeinsam variieren. Zum Bespiel sollte die Abschlussnote eines Studiums stets im Zusammenhang mit dem Studiengang und der Hochschule betrachtet werden. Im Gegensatz zur PFI trägt die SHAP Feature Importance diesem Umstand Rechnung. Auch sind Shapley Values, einmal berechnet, die Grundlage einer Bandbreite weiterer nützlicher XAI Methoden.

Eine Schwäche der Methode ist jedoch, dass sie aufwendiger zu berechnen ist als die PFI. Nur für bestimmte Arten von KI-Algorithmen (z.B. Entscheidungsbäume) gibt es effiziente Implementierungen. Es will also gut überlegt sein, ob für ein gegebenes Problem eine PFI-Analyse genügt, oder ob die SHAP Feature Importance zu Rate gezogen werden sollte.

Stärken	Schwächen
Wenig Spielraum für Manipulation der Ergebnisse	Berechnung ist rechenaufwendig
Berücksichtigt komplexe Interaktionen zwischen Variablen

Mit Accumulated Local Effects einzelne Variablen in den Fokus nehmen

Die Accumulated Local Effects (ALE) Methode ist eine Weiterentwicklung der Partial Dependence Plots (PDP), die sich großer Beliebtheit unter Data Scientists erfreuen. Beide Methoden haben das Ziel, den Einfluss einer bestimmten Variablen auf die Vorhersage des Modells zu simulieren. Damit können Fragen beantwortet werden wie: „Steigen mit zunehmender Berufserfahrung die Chancen auf eine Management Position?“ oder „Macht es einen Unterschied, ob ich eine 1.9 oder eine 2.0 in meinem Abschlusszeugnis habe?“. Im Gegensatz zu den vorherigen zwei Methoden trifft ALE also eine Aussage über die Entscheidungsfindung des Modells, nicht über die Relevanz bestimmter Variablen.

Im einfachsten Fall, dem PDP, wird eine Stichprobe von Beobachtungen ausgewählt und anhand dieser simuliert, welchen Einfluss z.B. eine isolierte Erhöhung der Berufserfahrung auf die Modellvorhersage hätte. Isoliert meint, dass dabei keine der anderen Variablen verändert wird. Der Durchschnitt dieser einzelnen Effekte über die gesamte Stichprobe liefert eine anschauliche Visualisierung (Abbildung 3, oben). Leider sind die Ergebnisse des PDP nicht besonders aussagekräftig, wenn korrelierte Variablen vorliegen. Am Beispiel der Hochschulnoten lässt sich das besonders gut veranschaulichen. So simuliert der PDP hierbei alle möglichen Kombinationen von Noten im Bachelor- und Masterstudium. Dabei entstehen leider Fälle, die in der echten Welt selten vorkommen, z.B. ein ausgezeichnetes Bachelorzeugnis und ein miserabler Masterabschluss. Der PDP hat kein Gespür für unsinnige Fälle, woran auch die Ergebnisse kranken.

Die ALE-Analyse hingegen versucht, dieses Problem durch eine realistischere Simulation zu lösen, die die Zusammenhänge zwischen Variablen adäquat abbildet. Dabei wird die betrachtete Variable, z.B. die Bachelor-Note, in mehrere Abschnitte eingeteilt (z.B. 6.0-5.1, 5.0-4.1, 4.0-3.1, 3.0-2.1 und 2.0-1.0). Nun wird die Simulation der Erhöhung der Bachelor-Note lediglich für Personen in der respektiven Notengruppe durchgeführt. Dies führt dazu, dass unrealistische Kombinationen nicht in die Analyse einfließen. Ein Beispiel für einen ALE-Plot findet sich in Abbildung 3 (unten). Hier zeigt sich anschaulich, dass der ALE-Plot einen negativen Einfluss der Berufserfahrung auf die Anstellungschance identifiziert, während dies dem PDP verborgen bleibt. Ist dieses Verhalten der KI erwünscht? Will man zum Beispiel insbesondere junge Talente einstellen? Oder steckt dahinter vielleicht eine versteckte Altersdiskriminierung? In beiden Fällen hilft der ALE-Plot dabei, Transparenz zu schaffen und ungewünschtes Verhalten rechtzeitig zu erkennen.

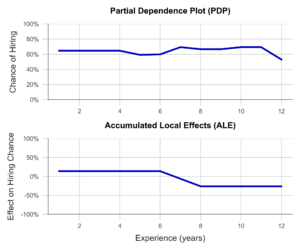
Abbildung 3– Partial Dependence Plot und Accumulated Local Effects am Beispiel einer Recruiting KI (Daten künstlich erzeugt).

Zusammenfassend ist der ALE-Plot eine geeignete Methode, um einen Einblick in den Einfluss einer bestimmten Variable auf die Modellvorhersage zu gewinnen. Dies schafft Transparenz für Nutzende und hilft sogar dabei, ungewünschte Effekte und Bias zu identifizieren und zu beheben. Ein Nachteil der Methode ist, dass der ALE-Plot stets nur eine Variable analysiert. Um also den Einfluss aller Variablen zu verstehen, muss eine Vielzahl von ALE-Plots generiert werden, was weniger übersichtlich ist als z.B. ein PFI- oder ein SHAP Feature Importance Plot.

Stärken	Schwächen
Berücksichtigt komplexe Interaktionen zwischen Variablen	Mit ALE lassen sich nur eine oder zwei Variablen pro Visualisierung analysieren
Wenig Spielraum für Manipulation der Ergebnisse

Mit Explainable AI Methoden Vertrauen aufbauen

In diesem Beitrag haben wir drei Explainable AI Methoden vorgestellt, die dabei helfen können, Algorithmen transparenter und interpretierbarer zu machen. Dies begünstigt außerdem, den Anforderungen des kommenden AI-Acts frühzeitig gerecht zu werden. Denn auch wenn dieser noch nicht verabschiedet ist, empfehlen wir auf Basis des Gesetzesentwurfs sich bereits jetzt mit der Schaffung von Transparenz und Nachvollziehbarkeit für KI-Modelle zu beschäftigen. Viele Data Scientists haben wenig Erfahrung in diesem Feld und benötigen Fortbildung und Einarbeitungszeit, bevor sie einschlägige Algorithmen identifizieren und effektive Lösungen implementieren können. Die weiterführende Beschäftigung mit den vorgestellten Methoden empfehlen wir daher in jedem Fall.

Mit der Permutation Feature Importance (PFI) und der SHAP Feature Importance haben wir zwei Techniken aufgezeigt, um die Relevanz bestimmter Variablen für die Vorhersage des Modells zu bestimmen. Zusammenfassend lässt sich sagen, dass die SHAP Feature Importance eine leistungsstarke Methode zur Erklärung von Black-Box-Modellen ist, die die Interaktionen zwischen Variablen berücksichtigt. Die PFI hingegen ist einfacher zu implementieren, aber weniger leistungsfähig bei korrelierten Daten. Welche Methode im konkreten Fall am besten geeignet ist, hängt von den spezifischen Anforderungen ab.

Auch haben wir mit Accumulated Local Effects (ALE) eine Technik vorgestellt, die nicht die Relevanz von Variablen, sondern sogar deren genauen Einfluss auf die Vorhersage bestimmen und visualisieren kann. Besonders vielversprechend ist die Kombination einer der beiden Feature Importance Methoden mit ausgewählten ALE-Plots zu ausgewählten Variablen. So kann ein theoretisch fundierter und leicht interpretierbarer Überblick über das Modell vermittelt werden – egal, ob es sich um einen Entscheidungsbaum oder ein tiefes Neuronales Netz handelt.

Die Anwendung von Explainable AI ist somit eine lohnende Investition – nicht nur, um intern und extern Vertrauen in die eigenen KI-Lösungen aufzubauen. Vielmehr gehen wir davon aus, dass der geschickte Einsatz interpretationsfördernder Methoden drohende Bußgelder durch die Anforderungen des AI-Acts vermeidet, rechtlichen Konsequenzen vorbeugt, sowie Betroffene vor Schaden schützt – wie im Fall von unverständlicher Recruitingsoftware.

Unserer kostenfreier AI Act Quick Check unterstützt Sie gerne bei der Einschätzung, ob eines Ihrer KI-Systeme vom AI Act betroffen sein könnte: https://www.statworx.com/ai-act-tool/

Quellen & Informationen:

https://www.faz.net/aktuell/karriere-hochschule/buero-co/ki-im-bewerbungsprozess-und-raus-bist-du-17471117.html (letzter Aufruf 03.05.2023)
https://t3n.de/news/diskriminierung-deshalb-platzte-amazons-traum-vom-ki-gestuetzten-recruiting-1117076/ (letzter Aufruf 03.05.2023)
Weitere Informationen zum AI Act: https://www.statworx.com/content-hub/blog/wie-der-ai-act-die-ki-branche-veraendern-wird-alles-was-man-jetzt-darueber-wissen-muss/
Statworx principles: https://www.statworx.com/content-hub/blog/statworx-ai-principles-warum-wir-eigene-ki-prinzipien-entwickeln/
Christoph Molnar: Interpretable Machine Learning: https://christophm.github.io/interpretable-ml-book/ Max Hilsdorf, Julia Rettig

Bildnachweis:
AdobeStock 566672394 – by TheYaksha

Einführung

Forecasts sind in vielen Branchen von zentraler Bedeutung. Ob es darum geht, den Verbrauch von Ressourcen zu prognostizieren, die Liquidität eines Unternehmens abzuschätzen oder den Absatz von Produkten im Einzelhandel vorherzusagen – Forecasts sind ein unverzichtbares Instrument für erfolgreiche Entscheidungen. Obwohl sie so wichtig sind, basieren viele Forecasts immer noch primär auf den Vorerfahrungen und der Intuition von Expert:innen. Das erschwert eine Automatisierung der relevanten Prozesse, eine potenzielle Skalierung und damit einhergehend eine möglichst effiziente Unterstützung. Zudem können Expert:innen aufgrund ihrer Erfahrungen und Perspektiven voreingenommen sein oder möglicherweise nicht über alle relevanten Informationen verfügen, die für eine genaue Vorhersage erforderlich sind.

Diese Gründe führen dazu, dass datengetriebene Forecasts in den letzten Jahren immer mehr an Bedeutung gewonnen haben und die Nachfrage nach solchen Prognosen ist entsprechend stark.

Bei statworx haben wir bereits eine Vielzahl an Projekten im Bereich Forecasting erfolgreich umgesetzt. Dadurch haben wir uns vielen Herausforderungen gestellt und uns mit zahlreichen branchenspezifischen Use Cases vertraut gemacht. Eine unserer internen Arbeitsgruppen, das Forecasting Cluster, begeistert sich besonders für die Welt des Forecastings und bildet sich kontinuierlich in diesem Bereich weiter.

Auf Basis unserer gesammelten Erfahrungen möchten wir diese nun in einem benutzerfreundlichen Tool vereinen, welches je nach Datenlage und Anforderungen jedem ermöglicht, erste Einschätzungen zu spezifischen Forecasting Use Cases zu erhalten. Sowohl Kunden als auch Mitarbeitende sollen in der Lage sein, das Tool schnell und einfach zu nutzen, um eine methodische Empfehlung zu erhalten. Unser langfristiges Ziel ist es, das Tool öffentlich zugänglich zu machen. Jedoch testen wir es zunächst intern, um seine Funktionalität und Nützlichkeit zu optimieren. Dabei legen wir besonderen Wert darauf, dass das Tool intuitiv bedienbar ist und leicht verständliche Outputs liefert.

Obwohl sich unser Recommender-Tool derzeit noch in der Entwicklungsphase befindet, möchten wir einen ersten spannenden Einblick geben.

Häufige Herausforderungen

Modellauswahl

Im Bereich Forecasting gibt es verschiedene Modellierungsansätze. Wir differenzieren dabei zwischen drei zentralen Ansätzen:

Zeitreihenmodelle
Baumbasierte Modelle
Deep Learning Modelle

Es gibt viele Kriterien, die man bei der Modellauswahl heranziehen kann. Wenn es sich um univariate Zeitreihen handelt, die eine starke Saisonalität und Trends aufweisen, sind klassische Zeitreihenmodelle wie (S)ARIMA und ETS sinnvoll. Handelt es sich hingegen um multivariate Zeitreihen mit potenziell komplexen Zusammenhängen und großen Datenmengen, stellen Deep Learning Modelle eine gute Wahl dar. Baumbasierte Modelle wie LightGBM bieten im Vergleich zu Zeitreihenmodellen eine größere Flexibilität, eignen sich aufgrund ihrer Architektur gut für das Thema Erklärbarkeit und haben im Vergleich zu Deep Learning Modellen einen tendenziell geringeren Rechenaufwand.

Saisonalität

Saisonalität stellt wiederkehrende Muster in einer Zeitreihe dar, die in regelmäßigen Abständen auftreten (z.B. täglich, wöchentlich, monatlich oder jährlich). Die Einbeziehung der Saisonalität in der Modellierung ist wichtig, um diese regelmäßigen Muster zu erfassen und die Genauigkeit der Prognosen zu verbessern. Mit Zeitreihenmodellen wie SARIMA, ETS oder TBATS kann die Saisonalität explizit berücksichtigt werden. Für baumbasierte Modelle wie LightGBM kann die Saisonalität nur über die Erstellung entsprechender Features berücksichtigt werden. So können Dummies für die relevanten Saisonalitäten gebildet werden. Eine Möglichkeit Saisonalität in Deep Learning-Modellen explizit zu berücksichtigen, besteht in der Verwendung von Sinus- und Cosinus-Funktionen. Ebenso ist es möglich die Saisonalitätskomponente aus der Zeitreihe zu entfernen. Dazu wird zuerst die Saisonalität entfernt und anschließend eine Modellierung auf der desaisonalisierten Zeitreihe durchgeführt. Die daraus resultierenden Prognosen werden dann mit der Saisonalität ergänzt, indem die genutzte Methodik für die Desaisonalisierung entsprechend angewendet wird. Allerdings erhöht dieser Prozess die Komplexität, was nicht immer erwünscht ist.

Hierarchische Daten

Besonders im Bereich Retail liegen häufig hierarchische Datenstrukturen vor, da die Produkte meist in unterschiedlicher Granularität dargestellt werden können. Hierdurch ergibt sich häufig die Anforderung, Prognosen für unterschiedliche Hierarchien zu erstellen, welche sich nicht widersprechen. Die aggregierten Prognosen müssen daher mit den disaggregierten übereinstimmen. Dabei ergeben sich verschiedene Lösungsansätze. Über Top-Down und Bottom-Up werden Prognosen auf einer Ebene erstellt und nachgelagert disaggregiert bzw. aggregiert. Mit Reconciliation-Methoden wie Optimal Reconciliation werden Prognosen auf allen Ebenen vorgenommen und anschließend abgeglichen, um eine Konsistenz über alle Ebenen zu gewährleisten.

Cold Start

Bei einem Cold Start besteht die Herausforderung darin Produkte zu prognostizieren, die nur wenig oder keine historischen Daten aufweisen. Im Retail Bereich handelt es sich dabei meist um Produktneueinführungen. Da aufgrund der mangelnden Historie ein Modelltraining für diese Produkte nicht möglich ist, müssen alternative Ansätze herangezogen werden. Ein klassischer Ansatz einen Cold Start durchzuführen, ist die Nutzung von Expertenwissen. Expert:innen können erste Schätzungen der Nachfrage liefern, die als Ausgangspunkt für Prognosen dienen können. Dieser Ansatz kann jedoch stark subjektiv ausfallen und lässt sich nicht skalieren. Ebenso kann auf ähnliche Produkte oder auch auf potenzielle Vorgänger-Produkte referenziert werden. Eine Gruppierung von Produkten kann beispielsweise auf Basis der Produktkategorien oder Clustering-Algorithmen wie K-Means erfolgen. Die Nutzung von Cross-Learning-Modellen, die auf Basis vieler Produkte trainiert werden, stellt eine gut skalierbare Möglichkeit dar.

Recommender Concept

Mit unserem Recommender Tool möchten wir die unterschiedlichen Problemstellungen berücksichtigen, um eine möglichst effiziente Entwicklung zu ermöglichen. Dabei handelt es sich um ein interaktives Tool, bei welchem man Inputs auf Basis der Zielvorstellung oder Anforderung und den vorliegenden Datencharakteristiken gibt. Ebenso kann eine Priorisierung vorgenommen werden, sodass bestimmte Anforderungen an der Lösung auch im Output entsprechend priorisiert werden. Auf Basis dieser Inputs werden methodische Empfehlungen generiert, die die Anforderungen an der Lösung in Abhängigkeit der vorliegenden Eigenschaften bestmöglich abdecken. Aktuell bestehen die Outputs aus einer rein inhaltlichen Darstellung der Empfehlungen. Dabei wird auf die zentralen Themenbereiche wie Modellauswahl, Pre-Processing und Feature Engineering mit konkreten Guidelines eingegangen. Das nachfolgende Beispiel gibt dabei einen Eindruck über die konzeptionelle Idee:

Der hier dargestellte Output basiert auf einem realen Projekt. Für das Projekt war vor allem die Implementierung in R und die Möglichkeit einer lokalen Erklärbarkeit von zentraler Bedeutung. Zugleich wurden frequentiert neue Produkte eingeführt, welche ebenso durch die entwickelte Lösung prognostiziert werden sollten. Um dieses Ziel zu erreichen, wurden mehrere globale Modelle mit Hilfe von Catboost trainiert. Dank diesem Ansatz konnten über 200 Produkte ins Training einbezogen werden. Sogar für neu eingeführte Produkte, bei denen keine historischen Daten vorlagen, konnten Forecasts generiert werden.

Um die Erklärbarkeit der Prognosen sicherzustellen, wurden SHAP Values verwendet. Auf diese Weise konnten die einzelnen Vorhersagen klar und deutlich anhand der genutzten Features erklärt werden.

Zusammenfassung

Die aktuelle Entwicklung ist darauf ausgerichtet ein Tool zu entwickeln, welches auf das Thema Forecasting optimiert ist. Durch die Nutzung wollen wir vor allem die Effizienz bei Forecasting-Projekten steigern. Durch die Kombination von gesammelten Erfahrungen und Expertise soll das Tool unter anderem für die Themen Modellierung, Pre-Processing und Feature Engineering Guidelines bieten. Es wird darauf ausgelegt sein, sowohl von Kunden als auch Mitarbeitenden verwendet zu werden, um schnelle und einfache Abschätzungen sowie methodische Empfehlungen zu erhalten. Eine erste Testversion wird zeitnah für den internen Gebrauch zur Verfügung stehen. Langfristig soll das Tool jedoch auch für externe Nutzer:innen zugänglich gemacht werden. Neben dem derzeit in der Entwicklung befindlichen technischen Output, wird auch ein weniger technischer Output verfügbar sein. Letzterer wird sich auf die wichtigsten Aspekte und deren Aufwände konzentrieren. Insbesondere die Business-Perspektive in Form von erwarteten Aufwänden und potenziellen Trade-Offs von Aufwand und Nutzen soll hierdurch abgedeckt werden.

Profitieren auch Sie von unserer Forecasting Expertise!

Wenn Sie Unterstützung bei der Bewältigung von vorliegenden Herausforderungen bei Forecasting Projekten benötigen oder ein Forecasting Projekt geplant ist, stehen wir gerne mit unserem Know-how und unserer Erfahrung zur Verfügung.

Vorname*

Nachname*

Telefon

E-Mail*

Firma*

Position*

Nachricht*

Mit dem Absenden stimme ich den Datenschutzbestimmungen zu.

Vielen Dank für Ihre Nachricht. Wir werden uns schnellstmöglich mit Ihnen in Verbindung setzen. Freundliche Grüße Ihr statworx Team

Marlon Schumacher

Bildnachweis:

AdobeStock 83282923 – Mego-studio

Die Kreuzvalidierung ist eine weit verbreitete Technik zur Bewertung der Generalisierbarkeit eines Machine-Learning-Modells. Hier bei STATWORX diskutieren wir oft über Evaluationsmetriken und darüber, wie wir sie effizient in unseren Data-Science-Workflow einbauen können. In diesem Blog-Beitrag stelle ich die Grundlagen der Kreuzvalidierung vor, gebe Hinweise zur Optimierung ihrer Parameter und zeige, wie man sie auf effiziente Weise von Grund auf selbst erstellen kann.

Grundlagen der Modellbewertung und Kreuzvalidierung

Die Kreuzvalidierung ist eine Technik zur Evaluation von Machine Learning-Modellen. Die zentrale Intuition hinter dieser Modellevaluierung besteht darin, herauszufinden, ob das trainierte Modell verallgemeinerbar ist, d. h., ob die Vorhersagekraft, die wir beim Training beobachten, auch bei ungesehenen Daten zu erwarten ist. Wir könnten das Modell direkt mit den Daten füttern, für die es entwickelt wurde, d. h. die es vorhersagen soll. Aber auch dann gibt es für uns keine Möglichkeit, zu wissen oder zu überprüfen, ob die Vorhersagen zutreffend sind.

Natürlich möchten wir eine Art Benchmark der Generalisierbarkeit unseres Modells haben, bevor wir es in die Produktion überführen. Daher besteht die Idee darin, die vorhandenen Trainingsdaten in einen tatsächlichen Trainingsdatensatz und einen Holdout-Testdatensatz aufzuteilen, die nicht zum Training verwendet wird und als „ungesehene“ Daten dient. Da dieser Testdatensatz Teil der ursprünglichen Trainingsdaten ist, haben wir eine ganze Reihe von „richtigen“ Ergebnissen, die wir überprüfen können. Zur Bewertung der Modellleistung kann dann eine geeignete Fehlermetrik wie der Root Mean Squared Error (RMSE) oder der Mean Absolute Percentage Error (MAPE) verwendet werden. Bei der Wahl der geeigneten Bewertungsmetrik ist jedoch Vorsicht geboten, da es Tücken gibt (wie in diesem Blogbeitrag meines Kollegen Jan beschrieben).

Bei vielen Algorithmen für Machine Learning können Hyperparameter angegeben werden, z. B. die Anzahl der Bäume in einem Random Forest. Die Kreuzvalidierung kann auch zum Tuning der Hyperparameter eines Modells genutzt werden, indem der Generalisierungsfehler verschiedener Modellspezifikationen verglichen wird.

Allgemeine Ansätze zur Modellevaluation

Es gibt Dutzende Techniken zur Modellevaluierung, die immer einen Kompromiss zwischen Varianz, Verzerrung und Rechenzeit darstellen. Bei der Bewertung eines Modells ist es wichtig, diese Kompromisse zu kennen, da die Wahl der geeigneten Technik in hohem Maße von der Problemstellung und den beobachteten Daten abhängt. Ich werde dieses Thema behandeln, nachdem ich zwei der gebräuchlichsten Techniken zur Modellevaluierung vorgestellt habe: den Train-Test-Split und die k-fache Kreuzvalidierung.

Bei der ersten Methode werden die Trainingsdaten nach dem Zufallsprinzip in eine Trainings- und eine Testeinheit aufgeteilt (Abbildung 1), wobei in der Regel ein großer Teil der Daten als Trainingsset beibehalten wird. In der Literatur werden am häufigsten Verhältnisse von 70/30 oder 80/20 verwendet, wobei das genaue Verhältnis von der Größe der Daten abhängt.

Der Nachteil dieses Ansatzes ist, dass diese einmalige zufällige Aufteilung dazu führen kann, dass die Daten in zwei sehr unausgewogene Teile aufgeteilt werden, was zu verzerrten Schätzungen des Generalisierungsfehlers führt. Dies ist besonders kritisch, wenn man nur über begrenzte Daten verfügt, da einige Merkmale oder Muster vollständig im Testteil landen könnten. In einem solchen Fall hat das Modell keine Chance, sie zu lernen, und seine Leistung wird möglicherweise unterschätzt.

train-test-split

Eine robustere Alternative ist die sogenannte k-fache Kreuzvalidierung (Abbildung 2). Hier werden die Daten gemischt und dann nach dem Zufallsprinzip in $k$ Teilmengen aufgeteilt. Der Hauptvorteil gegenüber dem Train-Test-Split besteht darin, dass jede der $k$ Partitionen iterativ als Testdatensatz (d. h. Validierungsmenge) verwendet wird, wobei die verbleibenden $k$ -Teile in dieser Iteration als Trainingsdaten dienen. Dieser Vorgang wird $k$ Mal wiederholt, sodass jede Beobachtung sowohl in den Trainings- als auch in den Testdaten enthalten ist. Die entsprechende Fehlermetrik wird dann einfach als Mittelwert aus allen $k$ Iterationen berechnet und ergibt den Kreuzvalidierungsfehler.

Dabei handelt es sich eher um eine Erweiterung des Train-Test-Splits als um eine völlig neue Methode: Das heißt, das Train-Test-Verfahren wird $k$ Mal wiederholt. Wenn $k$ z.B. so niedrig wie $k=2$ gewählt wird, erhält man zwar nur zwei Sets. Aber auch dieser Ansatz ist dem Train-Test-Split immer noch überlegen, da beide Teile iterativ für das Training ausgewählt werden, sodass das Modell die Chance hat, aus allen Daten zu lernen und nicht nur eine zufällige Teilmenge davon. Daher führt dieser Ansatz in der Regel zu robusteren Leistungsschätzungen.

k-fold-cross-validation

Wenn man die beiden Abbildungen oben vergleichtt, sieht man, dass eine Aufteilung von Training und Test mit einem Verhältnis von 80/20 einer Iteration einer 5-fachen (d.h. $k=5$ ) Kreuzvalidierung entspricht, bei der 4/5 der Daten für das Training und 1/5 für die Validierung zurückbehalten werden. Der entscheidende Unterschied ist, dass bei der k-fachen Kreuzvalidierung die Validierungsmenge in jeder der $k$ Iterationen verschoben wird. Beachte, dass eine k-fache Kreuzvalidierung robuster ist als die einfache Wiederholung der Aufteilung von Training und Test $k$ Mal: Bei der k-fachen Kreuzvalidierung wird die Aufteilung einmal vorgenommen und dann durch die Partitionen iteriert, wohingegen bei der wiederholten Aufteilung von Training und Test die Daten $k$ -mal neu aufgeteilt werden, wodurch möglicherweise einige Daten beim Training ausgelassen werden.

Wiederholte CV und LOOCV

Es gibt viele Varianten der k-fachen Kreuzvalidierung. Man kann zum Beispiel auch eine „wiederholte Kreuzvalidierung“ durchführen. Die Idee dahinter ist, dass sobald die Daten einmal in $k$ Partitionen aufgeteilt wurden, diese Aufteilung für das gesamte Verfahren gilt. Auf diese Weise besteht nicht die Gefahr, dass wir zufällig einige Teile ausschließen. Bei der Repeated CV wiederholst du diesen Prozess des Mischens und der zufälligen Aufteilung der Daten in $k$ Teilmengen eine gewisse Anzahl von Malen. Anschließend kannst du den Durchschnitt über die resultierenden Kreuzvalidierungsfehler der einzelnen Durchgänge bilden, um eine globale Leistungsschätzung zu erhalten.

Ein weiterer Spezialfall der k-fachen Kreuzvalidierung ist die „Leave One Out Cross-Validation“ (LOOCV), bei der du $k = n$ setzt. Das heißt, du verwendest in jeder Iteration eine einzige Beobachtung aus deinen Daten als Validierungsteil und die restlichen $n-1$ Beobachtungen als Trainingsmenge. Das klingt zwar nach einer sehr robusten Version der Kreuzvalidierung, aber von dieser Methode wird im Allgemeinen aus zwei Gründen abgeraten:

Erstens ist sie in der Regel sehr rechenintensiv. Für die meisten Datensätze, die beim angewandten Machine Learning verwendet werden, ist es weder erstrebenswert noch umsetzbar, das Modell $n-1$ Mal zu trainieren (obwohl es für sehr kleine Datensätze nützlich sein kann).
Zweitens: Selbst wenn man die Rechenleistung (und Zeit) hätte, um diesen Prozess durchzuführen, ist ein weiteres Argument, das von Kritiker:innen von LOOCV aus statistischer Sicht vorgebracht wird, dass der resultierende Kreuzvalidierungsfehler eine hohe Varianz aufweisen kann. Das liegt daran, dass das „Validierungsset“ nur aus einer einzelnen Beobachtung besteht, und je nach Verteilung deiner Daten (und möglichen Ausreißern) kann diese erheblich variieren.

Generell sollte man beachten, dass die Leistung von LOOCV sowohl in der wissenschaftlichen Literatur als auch in der breiteren Machine Learning Community ein etwas kontroverses Thema ist. Daher empfehle ich, sich über diese Debatte zu informieren, wenn man in Erwägung zieht, LOOCV zur Schätzung der Generalisierbarkeit eines Modells zu verwenden (siehe z. B. hier) und ähnliche Beiträge auf StackExchange). Wie so oft könnte die Antwort lauten: „Es kommt darauf an“. Bedenke auf jeden Fall den Rechenaufwand von LOOCV, der kaum von der Hand zu weisen ist (außer du hast einen winzigen Datensatz).

Der Wert von $k$ und der Kompromiss zwischen Verzerrung und Varianz

Wenn $k=n$ nicht (unbedingt) die beste Wahl ist, wie findet man dann einen geeigneten Wert für $k$ ? Es stellt sich heraus, dass die Antwort auf diese Frage auf den berüchtigten Bias-Variance Trade-Off hinausläuft. Warum ist das so?

Der Wert für $k$ bestimmt, in wie viele Partitionen die Daten unterteilt werden und damit auch die Größe (d.h. die Anzahl der Beobachtungen, die in jedem Teil enthalten sind). Wir wollen $k$ so wählen, dass ein ausreichend großer Teil unserer Daten in der Trainingsmenge verbleibt – schließlich wollen wir nicht zu viele Beobachtungen verschenken, die zum Trainieren unseres Modells verwendet werden könnten. Je höher der Wert von $k$ ist, desto mehr Beobachtungen werden bei jeder Iteration in die Trainingsmenge aufgenommen.

Nehmen wir zum Beispiel an, wir haben 1.200 Beobachtungen in unserem Datensatz, dann würde unser Trainingssatz bei $k=3$ aus $\frac{k-1}{k} * N = 800$ Beobachtungen bestehen, aber mit $k=8$ würde es 1.050 Beobachtungen umfassen. Je mehr Beobachtungen für das Training verwendet werden, desto eher approximiert man die tatsächliche Leistung des Modells (so als ob es auf dem gesamten Datensatz trainiert worden wäre) und desto geringer ist die Verzerrung – oder Bias – der Fehlerschätzung im Vergleich zu einem kleineren Teil der Daten. Doch mit zunehmendem $k$ nimmt die Größe der Validierungspartition ab, und die Fehlerschätzung reagiert in jeder Iteration empfindlicher auf diese wenigen Datenpunkte, wodurch die Gesamtvarianz steigen kann. Im Grunde genommen geht es darum, zwischen den „Extremen“ des Train-Test-Splits einerseits und LOOCV andererseits zu wählen. Die folgende Abbildung veranschaulicht schematisch (!) die Bias-Variance Performance und den Rechenaufwand der verschiedenen Kreuzvalidierungsmethoden.

bias-variance-tradeoff

Als Faustregel gilt: Mit höheren Werten für k nimmt die Verzerrung ab und die Varianz zu. Konventionell gelten Werte wie $k=5$ oder $k=10$ als guter Kompromiss und sind daher in den meisten Fällen des Machine Learning zum Quasi-Standard geworden.

„These values have been shown empirically to yield test error rate estimates that suffer neither from excessively high bias nor from very high variance.“

James et al. 2013: 184

Wenn du dich nicht besonders für den Prozess der Kreuzvalidierung interessierst, sondern ihn einfach in deinen Data Science Workflow integrieren willst (was ich dir sehr empfehle!), solltest du einen dieser Werte für $k$ wählen und es dabei belassen.

Implementierung der Kreuzvalidierung in

Apropos Integration der Kreuzvalidierung in deinen täglichen Arbeitsablauf – welche Möglichkeiten gibt es da? Glücklicherweise ist die Kreuzvalidierung ein Standardwerkzeug in beliebten Paketen für Machine Learning, wie z. B. dem Paket caret in R. Hier kannst du die Methode mit der Funktion trainControl festlegen. Im folgenden Skript trainieren wir einen Random Forest mit 10-facher Kreuzvalidierung auf dem iris Datensatz.

library(caret)

set.seed(12345)
inTrain <- createDataPartition(y = iris[["Species"]], p = .7, list = FALSE)

iris.train <- iris[inTrain, ]
iris.test <- iris[- inTrain, ]

fit.control <- caret::trainControl(method = "cv", number = 10)

rf.fit <- caret::train(Species ~ .,
                       data = iris.train,
                       method = "rf",
                       trControl = fit.control)

Wir definieren unsere gewünschte Kreuzvalidierungsmethode in der Funktion trainControl, speichern die Ausgabe im Objekt fit.control und übergeben dieses Objekt dann an das Argument trControl der Funktion train. Du kannst die anderen in diesem Beitrag vorgestellten Methoden auf ähnliche Weise definieren:

# Leave-One-Out Cross-validation:
fit.control <- caret::trainControl(method = "LOOCV", number = 10)

# Repeated CV (remember to specify the number of repeats!)
fit.control <- caret::trainControl(method = "repeatedcv", number = 10, repeats = 5)

Die altmodische Art: Die $k$ -fold Kreuzvalidierung von Hand implementieren

Data Science-Projekte können jedoch schnell so komplex werden, dass die vorgefertigten Funktionen in Machine Learning-Paketen nicht mehr geeignet sind. In solchen Fällen musst du den Algorithmus – einschließlich der Kreuzvalidierungstechniken – von Hand implementieren, zugeschnitten auf die spezifischen Projektanforderungen. Ich möchte dir ein provisorisches Skript zeigen, mit dem du eine einfache k-fache Kreuzvalidierung in R von Hand implementieren kannst (wir gehen das Skript hier Schritt für Schritt an; den gesamten Code findest du auf GitHub).

Daten simulieren, Fehlermetrik definieren und $k$ festlegen

# devtools::install_github("andrebleier/Xy")
library(tidyverse)
library(Xy)

sim <- Xy(n = 1000,
          numvars = c(2,2),
          catvars = 0,
          cor = c(-0.5, 0.9),
          noisevars = 0)

sim_data <- sim[["data"]]

RMSE <- function(f, o){
  sqrt(mean((f - o)^2))
}

k <- 5

Wir beginnen damit, die benötigten Pakete zu laden und einige Simulationsdaten mit 1.000 Beobachtungen mit dem Paket Xy() zu simulieren, das mein Kollege André entwickelt hat (siehe seinen Blogbeitrag über Regressionsdaten mit Xy simulieren). Da wir eine Art Fehlermaß zur Bewertung der Modellleistung benötigen, definieren wir unsere RMSE-Funktion, die ziemlich einfach ist: Der RMSE ist der Root Mean Squared Error, also die Wurzel aus dem Mittelwert des quadrierten Fehlers, wobei der Fehler die Differenz zwischen den gefitteten (fitted; f) und den beobachteten (observed; o) Werten ist – man kann die Funktion so ziemlich von links nach rechts lesen. Zuletzt geben wir unser k an, das im Beispiel auf den Wert 5 gesetzt ist und als einfacher Integer gespeichert wird.

Aufteilung der Daten

set.seed(12345)
sim_data <- mutate(sim_data,
                   my.folds = sample(1:k,
                                     size = nrow(sim_data),
                                     replace = TRUE))

Als nächstes unterteilen wir unsere Daten in $k$ folds. Hierfür fügen wir den Daten eine neue Spalte hinzu,my.folds: Wir ziehen eine Stichprobe (mit Zurücklegen) von 1 bis zum Wert von $k$ , in unserem Fall also 1 bis 5, und fügen jeder Zeile (Beobachtung) in den Daten zufällig eine dieser fünf Zahlen hinzu. Bei 1.000 Beobachtungen sollte jede Zahl etwa 200 Mal zugewiesen werden.

Training und Validierung des Modells

cv.fun <- function(this.fold, data){

  train <- filter(data, my.folds != this.fold)
  validate <- filter(data, my.folds == this.fold)

  model <- lm(y ~ NLIN_1 + NLIN_2 + LIN_1 + LIN_2,
              data = train)

  pred <- predict(model, newdata = validate) %>% as.vector()

  this.rmse <- RMSE(f = pred, o = validate$y)

  return(this.rmse)
}

Anschließend definieren wir „cv.fun“, das Herzstück unseres Kreuzvalidierungsverfahrens. Diese Funktion benötigt zwei Argumente: this.fold und data. Auf die Bedeutung von this.fold werde ich gleich zurückkommen, für den Moment setzen wir es einfach auf 1. Innerhalb der Funktion teilen wir die Daten in eine Trainings- und eine Validierungspartition auf, indem wir sie nach den Werten von my.folds und this.fold unterteilen: Jede Beobachtung mit einem zufällig zugewiesenen my.folds-Wert abweichend von 1 (also etwa 4/5 der Daten) geht in das Training. Alle Beobachtungen mit einem my.folds-Wert gleich 1 (die restlichen 1/5) bilden die Validierungsmenge. Zur Veranschaulichung passen wir dann ein einfaches lineares Modell mit dem simulierten Ergebnis und vier Prädiktoren an. Beachte, dass wir dieses Modell nur auf die train-Daten anwenden! Dann verwenden wir dieses Modell, um unsere Validierungsdaten vorherzusagen. Da wir für diese Teilmenge der ursprünglichen Trainingsdaten wahre Ergebnisse haben (darum geht es ja!), können wir unseren RMSE berechnen und ihn zurückgeben.

Iterieren durch die Foldings und Berechnen des CV-Fehlers

cv.error <- sapply(seq_len(k),
                   FUN = cv.fun,
                   data = sim_data) %>%
  mean()

cv.error

Zum Schluss verpacken wir den Funktionsaufruf von cv.fun in eine sapply()-Schleife – hier passiert die ganze Magie: Wir iterieren über den Bereich von k, so dass seq_len(k) uns in diesem Fall den Vektor [1] 1 2 3 4 5 liefert. Wir wenden jedes Element dieses Vektors auf cv.fun an. In der *apply()-Familie wird der Iterationsvektor immer als erstes Argument der aufgerufenen Funktion übergeben, so dass in unserem Fall jedes Element dieses Vektors zu einem Zeitpunkt an this.fold übergeben wird. Außerdem übermitteln wir unsere simulierten sim_data als Argument data.

Fassen wir kurz zusammen, was das bedeutet: In der ersten Iteration ist „this.fold“ gleich 1. Das bedeutet, dass unsere Trainingsmenge aus allen Beobachtungen besteht, bei denen my.folds nicht 1 ist, und die Beobachtungen mit dem Wert 1 bilden die Validierungsmenge (genau wie im Beispiel oben). In der nächsten Iteration der Schleife ist this.fold gleich 2. Folglich bilden die Beobachtungen mit den Werten 1, 3, 4 und 5 die Trainingsmenge und die Beobachtungen mit dem Wert 2 gehen in die Validierungsgruppe, und so weiter. Indem wir über alle Werte von k iterieren, erhalten wir das in Abbildung 2 gezeigte diagonale Muster, bei dem jede Datenpartition einmal als Validierungsmenge verwendet wird.

Zum Schluss berechnen wir den Mittelwert: Das ist der Mittelwert unserer k einzelnen RMSE-Werte und ergibt unseren Kreuzvalidierungsfehler. Und das war’s: Wir haben gerade unsere eigene Kreuzvalidierungsfunktion definiert!

Dies ist lediglich eine Vorlage: Du kannst jedes beliebige Modell und jede beliebige Fehlermetrik einfügen. Wenn du bis hierher durchgehalten hast, kannst du gerne selbst versuchen, eine wiederholte CV zu implementieren oder mit verschiedenen Werten für k herumzuspielen.

Fazit

Wie du siehst, ist es gar nicht so schwer, die Kreuzvalidierung selbst zu implementieren. Sie bietet dir eine große Flexibilität, um projektspezifische Anforderungen zu berücksichtigen, wie z. B. benutzerdefinierte Fehlermetriken. Wenn du nicht so viel Flexibilität brauchst, ist die Implementierung der Kreuzvalidierung in gängigen Machine Learning-Paketen ein Kinderspiel.

Ich hoffe, dass ich dir einen ausreichenden Überblick über die Kreuzvalidierung geben konnte und wie du sie sowohl in vordefinierten Funktionen als auch von Hand implementieren kannst. Wenn du Fragen, Kommentare oder Ideen hast, kannst du mir gerne eine E-Mail schicken.

Quellen

James, Gareth, Daniela Witten, Trevor Hastie, and Robert Tibshirani. 2013. An Introduction to Statistical Learning. New York: Springer.

Lukas Feick Lukas Feick

Der Vergleich von Prognosemethoden und Modellen über verschiedene Zeitreihen hinweg ist oft problematisch. Dieser Herausforderung sehen wir uns bei STATWORX regelmäßig gegenüber. Einheitenabhängige Maße wie der MAE (Mean Absolute Error) und der RMSE (Root Mean Squared Error) erweisen sich als ungeeignet und wenig hilfreich, wenn die Zeitreihen in unterschiedlichen Einheiten gemessen werden. Ist dies jedoch nicht der Fall, liefern beide Maße wertvolle Informationen. Der MAE ist gut interpretierbar, da er die durchschnittliche absolute Abweichung von den tatsächlichen Werten angibt. Der RMSE hingegen ist nicht so einfach zu interpretieren und anfälliger für Extremwerte, wird aber in der Praxis dennoch häufig verwendet.

$MAE\ =\frac{1}{n}\ \sum_{i\ =1}^{n}{|{\rm Actual}_i\ -\ {\rm Forecast}_i}|$

$\mathrm{RMSE=\ }\sqrt{\frac{\mathrm{1}}{\mathrm{n}}\mathrm{\ } \sum_{\mathrm{i\ =\ 1}}^{\mathrm{n}}{\mathrm{(}{\mathrm{Actual}}_\mathrm{i}\mathrm{-} {\mathrm{Forecast}}_\mathrm{i}\mathrm{)} }^\mathrm{2}}$

Eine der am häufigsten verwendeten Messgrößen, die dieses Problem vermeidet, heißt MAPE (Mean Absolute Percentage Error). Er löst das Problem der genannten Ansätze, da er nicht von der Einheit der Zeitreihe abhängt. Außerdem können Entscheidungsträger ohne statistisches Hintergrundwissen dieses Maß leicht interpretieren und verstehen. Trotz seiner Beliebtheit wurde und wird der MAPE immer noch kritisiert.

$MAPE\ =\frac{1}{n}\ \sum_{i\ =1}^{n}{|\frac{{\rm Actual}_i\ -\ {\rm Forecast}_i}{{\rm Actual}_i}|}*100$

In diesem Artikel bewerte ich diese kritischen Argumente und zeige, dass zumindest einige von ihnen höchst fragwürdig sind. Im zweiten Teil meines Artikels konzentriere ich mich auf die wahren Schwächen des MAPE. Im dritten Teil diskutiere ich verschiedene Alternativen und fasse zusammen, unter welchen Umständen die Verwendung des MAPE sinnvoll erscheint (und wann nicht).

Was dem MAPE alles FÄLSCHLICH vorgeworfen wird

Negative Fehler werden stärker bestraft als positive Fehler

Die meisten Quellen, die sich mit dem MAPE beschäftigen, weisen auf dieses „große“ Problem der Messung hin. Diese Aussage basiert hauptsächlich auf zwei verschiedenen Argumenten. Erstens wird behauptet, dass der Austausch des tatsächlichen Wertes mit dem prognostizierten Wert die Richtigkeit der Aussage beweist (Makridakis 1993).

Fall 1: ${Actual}_1$ = 150 & ${Forecast}_1$ = 100 (positive error)

${\rm APE}_1\ =\ |\frac{{\rm Actual}_1\ -\ {\rm Forecast}_1}{{\rm Actual}_1}|\ *100 =\ |\frac{150\ -\ 100}{150}|\ *100 =\ 33.33\ Percent$

Jan Fischer Jan Fischer

Ein paar hundert Meter von unserem Büro entfernt gibt es ein kleines Mittagslokal. Es gehört zu einer kleinen Kette, die sich auf selbst zusammenstellbare, verzehrfertige Salate spezialisiert hat. Als wir vor ein paar Jahren in unser neues Büro zogen, wurde dieser Salatlieferant schnell zu einem festen Bestandteil unseres Alltags. Im Laufe der Zeit hat sich das jedoch geändert. Wir essen immer noch regelmäßig dort, aber ich bin mir sicher, wenn man sich den STATWORX-bezogenen Umsatz ansieht, würde der Trend das Management nicht erfreuen, und die Frage ist, warum?
Die Antwort hat viel mit dem Auftreten neuer Konkurrenten, verbesserten Kochkünsten, ausgeklügelten Werbeaktionen und sicherlich auch mit der Preisgestaltung zu tun. Letztere – die Preisgestaltung – wird im Mittelpunkt dieser Serie stehen.
Bei der Analyse von Fragen der Preisgestaltung ist es oft von wesentlichem Interesse, ein Maß dafür zu haben, wie sich eine Preisänderung auf die Nachfrage auswirkt. Das Maß, auf das sich Ökonomen im Allgemeinen einigen, um diese Beziehung zu beschreiben, ist die Preiselastizität der Nachfrage, $\epsilon$ . Als relatives Maß ist es einheitsunabhängig, was es zu einem Gewinner macht. Die Elastizität ist definiert als die prozentuale Änderung der Menge geteilt durch die prozentuale Änderung des Preises:

$epsilon = frac{Delta qty/ qty}{Delta price/ price}$

Konzeptionell werden üblicherweise drei Bedingungen unterschieden: Elastizitätswerte von $<-1$ weisen auf eine „elastische Nachfrage“ hin. Das heißt, wenn man den Preis um ein Prozent erhöht, sinkt die Nachfragemenge um mehr als ein Prozent. Die beiden anderen Bedingungen sind Nachfrageelastizitäten von $>-1$ , in diesem Fall spricht man von „unelastischer Nachfrage“ und dem Fall, dass die Elastizität gleich -1 ist. Dies wird als „einheitselastische Nachfrage“ bezeichnet.

Es wäre sehr hilfreich, wenn wir die tatsächliche Preiselastizität der Nachfrage für unsere Salatbar ableiten könnten. Mit einem zuverlässigen Elastizitätswert in der Hand können wir Fragen beantworten wie: Wie viele Salate können wir bei einem bestimmten Preis voraussichtlich verkaufen? Wie wirkt sich eine Preisänderung von 10 % auf die Nachfrage aus? Mit diesem Wissen wäre es möglich, die Preisgestaltung als Instrument zu nutzen, um verschiedene KPIs für das Salatgeschäft zu erreichen. Letztendlich kann die Salatbar ihren Preis anpassen, um den Gewinn zu maximieren oder den Umsatz zu steigern – je nach ihren strategischen Zielen.

Die Feinheiten der Ableitung dieser Preiselastizitäten der Nachfrage mit Regressionen sind das Thema dieses kurzen Blogs. Die Situation unseres Salatanbieters ist ein anschauliches Beispiel dafür, wie wir die Preiselastizität berechnen können und wie sie zur Anpassung der eigenen Preisstrategie genutzt werden kann.

Einrichtung

Um es vorweg zu nehmen – obwohl dieser Salatverkäufer existiert und tatsächlich ein integraler Bestandteil der STATWORX-Nahrungskette ist, sind alle Daten, mit denen wir arbeiten, erfunden. Sie beschreiben, wie ich mir die Marktsituation dieses kleinen Salatanbieters vorstelle. Mit jedem neuen Beitrag, in dem wir komplexere Themen untersuchen, werden wir tiefer in die Welt der Salatverkäufer eintauchen.

Die Frage dieses Blogbeitrags ist einfach: Wie können wir mit Hilfe der linearen Regression Preiselastizitäten ableiten? Um dies zu untersuchen, benötigen wir Informationen über historische Preise und Verkäufe. Zu Beginn werden keine Konkurrenz, keine Alternativprodukte in den Geschäften, keine neuen Werbeaktionen, keine saisonalen Effekte oder ähnliches berücksichtigt.
Die täglichen Verkaufspreise der letzten zwei Jahre wurden für unsere kleine Salatbar simuliert, indem zufällig Preise zwischen 5,59 € und 9,99 € ausgewählt wurden – natürlich keine großartige Preisstrategie, aber für die Zwecke dieses Beitrags reicht sie aus. Zur Ableitung der Verkäufe wurde eine multiplikative Nachfragefunktion verwendet, der ein gewisser Zufallsfaktor hinzugefügt wurde. Und damit sind wir mit der Simulation der Daten fertig. Weitere Einzelheiten finden Sie im Code auf unserer Github-Seite.

Berechnung der Elastizität der Nachfrage

Wir wollen wissen, wie sich eine lineare Regressionsfunktion zur Elastizität verhält. Es stellt sich heraus, dass dies davon abhängt, wie die Variablen transformiert wurden. Es ist möglich, die Elastizität – ein Faktor der relativen Veränderung – in fast jeder Situation abzuleiten. Hier finden Sie die vier häufigsten Umformungen.

Transformation	Function	Elasticity
Level-Level	$Y = a+bX$	$epsilon=b*frac{X}{Y}$
Log-Level	$log(Y) = a+bX$	$epsilon=b*X$
Level-Log	$Y = a+b*log(X)$	$epsilon=frac{b}{Y}$
Log-Log	$log(Y) = a+b*log(X)$	$epsilon=b$

Abhängig von der Transformation der Variablen vor der Regression sind unterschiedliche Transformationen nach der Regression erforderlich, um die Elastizitätswerte zu ermitteln. Die obige Tabelle zeigt, dass die Elastizität im Falle eines log-log-Modells ein konstanter Wert über die gesamte Nachfragekurve ist, während sie in allen anderen Fällen vom spezifischen aktuellen Preis und/oder der Nachfrage abhängig ist. Dies bedeutet, dass die Wahl des Modells einen Hinweis auf die angenommene Nachfragekurve gibt. Eine falsche Wahl führt zu einem falsch spezifizierten Modell.

Das ist gut zu wissen, aber welches Modell sollte man verwenden? Um dies zu beurteilen, habe ich einfach jedes dieser vier Modelle durchgespielt. Die Ergebnisse finden Sie in der Tabelle unten, aber sie sind nichts, was man jemals in der realen Welt finden wird, da alle Effekte hoch signifikant sind und der $R^2$ für eine soziale oder wirtschaftliche Analyse lächerlich hoch ist. Dies ist beabsichtigt, da kaum Zufälligkeiten hinzugefügt wurden. Darüber hinaus waren die Daten so angelegt, dass das Log-Log-Modell prädestiniert war, das „Gewinnmodell“ zu erzeugen.

Model	Intercept	Price Variable	$varnothing$ Elasticity	$R^2$
Level-Level	439.58 (3.2)	-38.57 (0.42)	-2.50	0.84
Log-Level	6.59 (0.01)	-0.23 (0.01)	-1.63	0.95
Level-Log	671.22 (3.53)	-265.66 (1.83)	-2.11	0.93
Log-Log	7.86 (0.01)	-1.52 (0.01)	-1.51	0.97

Das Argument ist nicht, dass ein Log-Log-Modell das beste Modell zur Ableitung von Elastizitäten ist. Allerdings gibt es starke mikroökonomische Argumente dafür, warum das Log-Log-Modell das sinnvollste Modell zur Beschreibung der Nachfrageelastizität ist. Die zugrunde liegende Nachfragekurve beschreibt die Nachfrage am ehesten so, wie Ökonomen sie vermuten. Sie stellt sicher, dass die Nachfrage nicht unter Null sinken kann, wenn der Preis steigt, und dass auf der anderen Seite die Nachfrage exponentiell wächst, wenn der Preis sinkt. Die Ableitbarkeit eines konstanten Elastizitätswertes ist jedoch, wie bereits erwähnt, ihre wünschenswerteste Eigenschaft. Diese Tatsache macht es viel einfacher, die Elastizität zur Optimierung der Preisgestaltung einzusetzen.

Dennoch kann die empirische Analyse uns dazu bringen, andere Preis-Nachfrage-Beziehungen anzunehmen. Die folgende Grafik zeigt dies auf anschauliche Weise. Die Legende der Grafik ordnet die Modelle in aufsteigender Reihenfolge ihrer Eignung. Bei der Betrachtung der einzelnen Diagramme wird deutlich, warum das Level-Log-Modell besser abschneidet als das Level-Level-Modell, und warum das Log-Level-Modell das Level-Log-Modell übertrifft und so weiter. Die nicht-lineare Beziehung zwischen Preis und Nachfrage, die wir durch die Verwendung einer multiplikativen Nachfragekurve eingeführt haben, wird am besten durch das Log-Log-Modell beschrieben. Hätte ich eine additive Nachfragekurve verwendet, wäre die Rangfolge andersherum gewesen. Das Argument lautet also, dass die Wahl des Modells unter bestimmten Umständen einen erheblichen Einfluss haben kann.

elasticity regression comp

Für die Anwendung in der Praxis müssen wir uns der funktionalen Form, die durch die von uns gewählte Regression angezeigt wird, sehr bewusst sein. Die Auswirkungen können schwerwiegende Folgen haben. Die Elastizität, mit der die Daten erzeugt wurden, betrug -1,5. Um zu veranschaulichen, wie sich die Wahl des Modells auf die geschätzte Elastizität auswirken kann, habe ich die durchschnittlichen Elastizitäten für Modelle auf Niveau-, Log-Level- und Level-Level-Niveau berechnet und sie mit dem Preiskoeffizienten des Log-Log-Modells verglichen. Dies ist zwar eine etwas zu starke Vereinfachung, aber der Punkt bleibt bestehen: Die Ergebnisse sind sehr unterschiedlich, was Konsequenzen hat, wenn man versucht, die abgeleiteten Elastizitäten zu nutzen. Auf der Grundlage der grafischen Analyse und der Modellinformationen würden wir jedoch zu dem Schluss kommen, dass das Log-Log-Modell am besten abschneidet, so dass wir so vorgehen können, wie es die Theorie vorsieht.

Preis-Optimierung

evor wir zum Schluss kommen, wollen wir uns kurz ansehen, wie wir die Elastizität nutzen können, um die erratische Preisstrategie des kleinen Salatverkäufers zu verbessern (meine zufällige tägliche Preisänderung). Dazu müssen wir die Kostenfunktion der Salatbar kennen. Glücklicherweise kennen wir sie: Die Salatbar hat für jeden Tag, an dem sie geöffnet ist, Fixkosten von etwa 300 €. Die Zubereitung eines einzelnen Salats kostet etwa 2,50 € pro Salat. Die Kostenfunktion lautet also:

$€€TotalCost = 300€ + SaladesSold * 2.50€$

Die Mikroökonomie lehrt uns, dass Fixkosten bei der Berechnung von elastizitätsbasierten, margenoptimierten Preisen keine Rolle spielen. Ich erspare dir die Details, aber die Funktion zur Berechnung des optimierten Preises lautet letztendlich wie folgt:

$OptimalPrice = frac{Elasticity*CostPerSalad}{1+Elasticity}$

Unter Anwendung der aus dem Log-Log-Modell abgeleiteten Elastizität ergibt sich ein vorgeschlagener optimaler Preis, der irgendwo zwischen 7,21€ und 7,47€ liegt. Die Schätzung liegt bei 7,34 €. Anstatt seinen Preis täglich willkürlich zu ändern, ist es am besten, sich an Preise in diesem Bereich zu halten. Der Salatverkäufer kann davon ausgehen, dass er jeden Tag etwa 125 Salate verkauft, was ihm einen täglichen Gewinn zwischen 287 € und 320 € sichert.

KPIs	Lowerbound Elasticity	Exp. Elasticity	Upperbound Elasticity
Elasticity	-1.51	-1.52	-1.54
Opt. Price	7.43€	7.30€	7.17€
Quantity	126	125	125
Profit	319€	302€	285€

Dies ist eine gewagte Aussage. Mit den tatsächlichen Beispieldaten wäre die Schlussfolgerung in Ordnung. Aber in der Praxis sind solche perfekten Regressionsergebnisse mit so wenig Unsicherheit unrealistisch. Und genau hier wird es heikel. Zur Veranschaulichung dieses Punktes habe ich den Standardfehler von fast nicht vorhanden auf 0,15 angepasst. Die Ergebnisse sollten immer noch hochsignifikant sein, aber wenn man sich die nachstehende Tabelle ansieht, wäre man über die Folgen solch kleiner Änderungen überrascht.

KPIs	Lowerbound Elasticity	Exp. Elasticity	Upperbound Elasticity
Elasticity	-1.23	-1.52	-1.82
Opt. Price	13.51€	7.30€	5.57€
Quantity	106	125	114
Profit	864€	302€	51€

Die Gewissheit, mit der wir den optimalen Preis vorgeschlagen haben, war sehr unbegründet. In diesem Beispiel ist die Spanne für die Elastizität trotz der größeren Unsicherheit immer noch relativ klein. Die sich daraus ergebende Preisspanne für den idealen Preis liegt jedoch zwischen 5,58 € und 13,73 €, was kein sehr präziser Vorschlag ist. Die Preisspanne liegt sogar über dem höchsten Preis, den der kleine Salatverkäufer jemals zu setzen wagte. Die Folgen sind gravierend: Der resultierende Gewinn schwankt fast um das Sechzehnfache zwischen dem höchsten und dem niedrigsten Preis.

Um das Offensichtliche zu verdeutlichen: Der dargestellte Ansatz zur Elastizitätsberechnung ist nur die Spitze des Eisbergs. Das bedeutet, dass wir Zeit in die Verbesserung des derzeitigen Ansatzes investieren müssen. Die nächsten Beiträge werden sich auf intervenierende Faktoren wie Werbemaßnahmen und ähnliche Produkte konzentrieren. Daniel Lüttgau Daniel Lüttgau

Wie kann man Preiselastizität bestimmen? Die Antwort auf diese Frage ist nicht eindeutig, sondern fallspezifisch. Es gibt viele Verfahren, um Preiselastizität empirischzu bestimmen. DirekteExpertenbefragungen, Kundenbefragungen, indirekte Kundenbefragungen durch Conjoint Analysen und vielfältige experimentelle Testmethoden.

Wenn die Datenlage es erlaubt, wenden wir Methoden an, die auf historischen Marktdaten basieren. Unterfüttert mit Daten zu Faktoren, wie Wettbewerbspreise, Werbeinformationen etc., lassen sich hier durch am erfolgreichsten die entscheidenden Wirkungsmechanismen für eine dynamische und automatisierte Preisgestaltung identifizieren.

In drei Blogposts sollen die verschiedenen Verfahren beleuchtet und ihre Vor- und Nachteile aufbereitet werden. Im vergangen ersten Teil wurden befragungsbasierten Verfahrenbesprochen. In diesem zweiten Teil wird der Fokus auf experimentellen Methoden und Conjoint Analysen liegen. Im darauf folgenden und abschließenden Post sollen gängige regressionsbasierte Verfahren Thema sein.

Die im vorherigen Blogbeitrag beschrieben Expertenbefragungen und direkte Kundenbefragungen sind in vielerlei Hinsicht schwierig. Experteninterviews vernachlässigen systematisch die Kundenperspektive. Kundenbefragungen sind inhaltlich problematisch, da sie fast zwingend eine isolierte Fokussierung auf die Preissetzung bewirken. Dies steht im Widerspruch zum eigentlichen Kaufprozess, der viel wahrscheinlicher einer Kosten-Nutzen-Abwägung entspricht.

Indirekte Verfahren

Um diesen Problemen auszuweichen, wird daher häufig auf indirekte Befragungsmethoden zurückgegriffen. Durch indirekte Befragungsverfahren sollen die Kaufsituation und die Kundenentscheidung realistischer abgebildet werden, als dies durch Befragungen möglich ist. Ein zentrales Konzept sind dabei Conjoint Analyse Verfahren. Conjoint Analysen sind ein zentrales und etabliertes Marketinginstrument mit vielfältigen auf die jeweilige Problemstellung zugeschnittene Varianten.

Grundsätzlich sollen Conjoint Analysen dabei helfen, die tatsächlichen Abwägungen und Präferenzen von Kunden zwischen verschiedenen Bedürfnissen besser nachzuvollziehen. Durch ein umfassenderes Verständnis der Kundenpräferenzen sollen dann Rückschlüsse auf die konkrete Fragestellung abgeleitet werden. Prinzipiell können so durch Conjoint Analysen vielfältige und komplexe Fragestellungen beantwortet werden.

Um die Zahlungsbereitschaft von Kunden abzufragen, werden Kunden z.B. verschiedene sogenannte Produkt-Preis-Profile zur Auswahl gestellt. Die verschiedenen Auswahlmöglichkeiten unterscheiden sich hinsichtlich im Voraus definierter Merkmale und bzgl. des Preises. Die Teilnehmer sind aufgefordert, zwischen diesen Alternativen zu wählen und Ihre Präferenzen darzulegen. Basierend auf diesen Präferenzaussagen werden die Wirkungen des Preises und der verschiedenen Produktmerkmale herausgearbeitet.

Der Erfolg von Conjoint Verfahren hängt wesentlich von den vorbereitenden Schritten bei der Produkt-Preis-Profi-Gestaltung ab. Eine Vielzahl von Entscheidungen müssen getroffen werden, z.B.:

Wie viele verschiedene Merkmale sollen verglichen werden? Dies ist nicht trivial, denn es kann schnell unübersichtlich werden. Entscheidet man sich für nur 3 Merkmale mit jeweils 3 Ausprägungen, so konfrontiert man den Konsumenten bereits mit bis zu 27 Alternativen. Wollte man hier mit Paarvergleichen arbeiten, dann müsste sich der Teilnehmer theoretisch durch 351 Paarvergleich arbeiten. In der Praxis werden natürlich
Wie viele Ausprägungen sollen je Merkmal auswählbar sein? Studien zu Folge werden Produkte mit mehr Auswahlmöglichkeiten von Teilnehmern als wichtiger erachtet. Es gibt viele ähnliche Beispiele dafür wie das Testdesign das Ergebnis beeinflusst. Problematisch wird dies, wenn die Wirkung des Testdesigns den tatsächlichen Kaufprozess entstellt.
Wie sollen den Teilnehmern die verschiedenen Alternativen präsentiert werden? Sollen alle Alternativen mit ihren unterschiedlichen Preisen gleichzeitig präsentiert werden (Vollprofile) oder sind Paarvergleiche besser? Vollprofile sind realitätsnäher, aber konfrontieren den Teilnehmer mit einer komplexeren Problemstellung, wodurch evtl. keine klaren Ergebnisse abgeleitet werden können.

Der Anwender von Conjoint Verfahren wird mit der komplexen Anforderungspalette konfrontiert, der man bei Experimenten oder bei der Fragebogenausgestaltung ebenfalls begegnet. Dennoch sind Conjoint Analysen ein beliebtes und häufig angewandtes Verfahren. Insbesondere Computergestützte Methoden helfen inzwischen die Komplexität zu reduzieren.

Ähnlich wie die anderen bereits beschriebenen Verfahren sind Conjoint-Analysen kein Instrument, das für ein fortlaufendes systematisches Elastizitäts-Monitoring geeignet ist. Conjoint Verfahren können für explorative Analysen, z.B. im Fall von Produktneueinführungen, ein sehr nützliches Instrument darstellen. Gilt es aber ein fortlaufendes, reaktives Preisgestaltungsinstrument zu entwickeln, so wird das Verfahren an seine Grenzen stoßen, insbesondere dann, wenn man ein breites Produktsortiment hat.

Experimente

Bei Experimenten werden Kunden(-Gruppen) in realen oder nachgestellten Kaufsituationen (Feld-bzw. Laborexperimente) verschiedene Preisalternativen vorgegeben. Aus dem Kaufverhalten der Testteilnehmer werden Rückschlüsse bzgl. des Effektes des Preises auf den Absatz abgeleitet. Ähnlich wie bei Conjoint Analysen gibt es bei der Ausgestaltung solcher Tests viele Vorgehensmöglichkeiten. Insbesondere der E-Commerce bietet vielfältige Anwendungsmöglichkeiten, da viele zusätzliche transaktionsspezifische Informationen bei der statistischen Auswertung des Experiments hinzugezogen werden können. Doch auch im Brick-And-Mortar-Bereich können durch klassische Store-Tests wichtige Rückschlüsse auf produktspezifische Zahlungsbereitschaften gewonnen werden.

Letztlich gibt es fast keine Grenzen bei der Ausgestaltung von preisbezogenen Experimenten, insbesondere dann, wenn auch Laborexperimente in Frage kommen. Hier stellt sich immer die Frage nach der externen Validität dieser Experimente. Künstliche Situationen können atypisches Verhalten verursachen. Ebenso kann es schwierig sein, aus den Erkenntnissen des Experiments praxisrelevante Schlüsse zu ziehen.

Ebenfalls problematisch sind die hohen Kosten, die mit Experimenten einhergehen. Insbesondere mit Feldexperimenten greift man direkt in das aktive Geschäft ein. Jede Preissenkung kann mit Profitverlust einhergehen, jede Preiserhöhung kann Absatzverluste bedeuten.

In unseren Projekten mit Kunden nutzen wir Feldexperimente als Validierungswerkzeug für unsere auf Marktdaten basierten Analyseverfahren. Modellgesteuerte Feldexperimente können genutzt werden, um die Prognosegüte eines Modells zu evaluieren und dessen Schwächen aufzudecken.

Alle bisher beschriebenen Verfahren haben ihre Funktion und können bei entsprechenden Rahmenbedingungen sinnvoll und richtig sein. Wenn die Datenlage es aber erlaubt, wenden wir Methoden an, die auf historischen Marktdaten basieren. Im abschließenden Post sollen gängige regressionsbasierte Verfahren Thema sein. Daniel Lüttgau Daniel Lüttgau

Wie kann man Preiselastizität bestimmen? Die Antwort auf diese Frage ist nicht eindeutig, sondern fallspezifisch. Es gibt viele Verfahren, um Preiselastizität empirisch zu bestimmen. Direkte Expertenbefragungen, Kundenbefragungen, indirekte Kundenbefragungen durch Conjoint Analysen und vielfältige experimentelle Testmethoden.

Wenn die Datenlage es erlaubt, wenden wir Methoden an, die auf historischen Marktdaten basieren. Unterfüttert mit Daten zu Faktoren, wie Wettbewerbspreise, Werbeinformationen etc., lassen sich hierdurch am erfolgreichsten die entscheidenden Wirkungsmechanismen für eine dynamische und automatisierte Preisgestaltung identifizieren.

In drei Blogposts sollen die verschiedenen Verfahren beleuchtet und ihre Vor- und Nachteile aufbereitet werden. Der heutige erste Teil beginnt mit befragungsbasierten Verfahren. Der zweite wird sich mit experimentellen Methoden und Conjoint Analysen beschäftigen. Im darauf folgenden und abschließenden Post sollen gängige regressionsbasierte Verfahren Thema sein.

Expertenbefragungen

Der auf Befragungen basierende Methodenbereich gliedert sich in Expertenbefragungen und verschiedene Verfahren der Kundenbefragung. Wir beginnen mit Expertenbefragungen. Dabei werden Fachleute mit umfassendem Wissen über den Markt oder ein spezielles Marktsegment, in dem das Unternehmen agiert, zur Preiswirkung befragt. Naheliegende Ansprechpartner sind vertriebsnahe Manager, Mitarbeitern aus dem Vertrieb oder Marketing, aber auch externe Fachleute und Berater. Methodisch kann zwischen unstrukturierten, freien Interviews und strukturierten, häufig Workshop basierten, in klare Vorgehensschritte untergliederte Verfahren gewählt werden.

Expertenbefragungen sind in der Regel günstiger und weniger zeitintensiv als Kundenbefragungen. In der Hoffnung, dass Fachleute markttransformierende Ereignisse früher und besser erkennen als andere Verfahren, werden Expertenbefragungen gelegentlich auch unterstützend zu anderen Methoden durchgeführt.

Ein Vorteil von Expertenbefragungen ist, dass sie auch in Momenten hoher Ungewissheit zu Ergebnissen führen. Vollständig unerprobter Preisstrategien oder neue Marktsituationen durch neue Wettbewerber oder veränderte Kundenbedürfnisse sind in der Regel nur mit Hilfe von Expertenurteilen abzubilden. Unklar ist aber, welchen Wert diese Ergebnisse haben, denn der mit unbekannten Situationen einhergehenden Unsicherheit sind auch die Experten ausgesetzt.

Darüber hinaus kämpfen Expertenbefragungen mit einer Reihe von Problemen: Es gelingt durch sie nicht, die Kundenperspektive mit einzubeziehen. Außerdem können Experten als Folge von systematisch falschen Annahmen oder lange gültigen, aber veralteten,Paradigmen falsche Schlüsse ziehen. Experten kommen außerdem häufig zu stark divergierenden Prognosen, die dann schwer vereinbar sind.

Insgesamt gilt, dass Expertenbefragungen für ein fortlaufendes Elastizitäten-Monitoring eher ungeeignet sind. Andere analytische Verfahren sind in höherer Frequenz und größerem Umfang durchführbar. In schnelllebigen Marktumfeldern oder für Akteure mit großen Produktsortimenten sind dies entscheidende Nachteile von Expertenbefragungen.

Kundenbefragungen

Bei direkten Befragungen werden Kunden durch Fragen wie „Zu welchem Preis würden Sie dieses Produkt gerade noch kaufen?“ zu ihrer Zahlungsbereitschaft befragt. Die Angaben werden genutzt, um Elastizitätswerte abzuleiten. Durch eine bewusste Fragekonstruktion oder eine gezielte Abfolge können zusätzliche Sachverhalte abgefragt werden. Die ergänzende Frage: „Ab welchem Preisunterschied würden Sie von Produkt X zu Produkt Y wechseln?” erlaubt beispielsweise die gezielte Abfrage von Kreuzelastizitäten zwischen spezifischen Substituten.

Direkte Befragungen sind in vielerlei Hinsicht schwierig. Insbesondere im Kontext von Konsumgütern mit einer Vielzahl an Produkten und Alternativen wird das Abfragen von Zahlungsbereitschaften aufwendig. Inhaltlich problematisch ist die fast zwingend isolierte Fokussierung auf die Preissetzung. Dies steht im Widerspruch zum eigentlichen Kaufprozess, der viel wahrscheinlicher einer Kosten-Nutzen-Abwägung entspricht. Studien weisen auch auf eine Diskrepanz zwischen tatsächlichem und in Umfragen bekundeten Verhalten hin.

Um diesen Problemen auszuweichen, wird daher häufig auf indirekte Befragungsmethoden in Form von Conjoint Analyse oder experimentelle Testdesigns zurückgegriffen. Durch diese Verfahren sollen die Kaufsituation und die Kundenentscheidung realistischer abgebildet werden, als dies durch Befragungen möglich ist. Diese alternativen Verfahren sind Thema des nächsten Beitrags. Daniel Lüttgau Daniel Lüttgau

In diesem Blogeintrag aus der „Gut in Form”-Reihe wird gezeigt, wie sich Datenreshapes in R, Stata und SPSS umsetzten lassen. Diese Datenreshapes dienen dazu, die vorliegenden Daten zu transformieren und so die optimale Darstellung zu erhalten, wenn pro Einheit mehrere Informationen zu einer Begebenheit vorliegen.

Was vielleicht etwas kompliziert klingt, soll anhand eines Beispiels erläutert werden: Es soll ein Datensatz erstellt werden, der Informationen zur Tagesdurchschnittstemperatur am 01.01.2018 in allen europäischen Hauptstädten enthält. Die Städte repräsentieren also die Einheiten, die am Anfang des Beitrags erwähnt werden, die Temperaturen entsprechen den Informationen. Hat man nur Informationen zu einem Tag, so gibt es nur einen vernünftigen Weg die Daten darzustellen. Es gibt zwei Variablen, Stadt und Temperatur, und jede Stadt steht in einer eigenen Zeile.

Hat man jedoch pro Stadt Informationen für zwei Tagezeiten (vormittags/nachmittags), so stellt sich die Frage nach der Darstellung. Man spricht hier von einem sogenannten Panel-Design. Generell gibt es zwei Formate, um dies darzustellen: das Long- und das Wide-Format. Die Transformation zwischen den Formaten wird auch Reshape genannt.

Beim Long-Format wird jede einzelne Information/Messung in einer eigenen Zeile dargestellt. Für unser kleines Beispiel heißt das, dass zusätzlich zur Stadt- und Temperatur-Variable eine neue hinzukommt, die Tageszeit, an dem die Temperatur gemessen wurde, angibt. Pro Stadt können im Datensatz so mehrere Fälle (Zeilen) bestehen. In der untenstehenden Darstellung ist dies für mögliche Temperatur in einem Ausschnitt dargestellt.

Beim Wide-Format existiert für jede Einheit nur eine Zeile. Das bedeutet jedoch auch, dass es nicht mehr nur eine, sondern mehrere Variablen zur Information gibt. Für das Beispiel heißt das konkret, dass für jede Tageszeit, zu der Informationen vorliegen, eine Variable angelegt werden muss. Im Gegensatz zum Long-Format geht die Struktur der Daten eher in die Breite, daher auch die Bezeichnung als „Wide“.

datenaufbereitung beispiel

Natürlich kann es auch vorkommen, dass nicht zu allen Begebenheiten/Messungen Informationen für alle Einheiten vorliegen. Im Long-Format fällt dies nicht eindeutig auf, im Wide-Format dagegen eher. Für die Datenaufbereitung ist dies unerheblich. Wie methodisch mit solch einem unbalanciertem Design umgegangen wird, ist nicht Bestandteil dieser Blogreihe.

Datensatz

Der Datensatz wurde bereits in den beiden vorherigen Beiträgen zu den Themen Datenimport und Datentypen vorgestellt. Darin ist für verschiedene STATWORX Mitarbeiter, deren realer Name durch den jeweiligen Lieblingsstatistiker ersetzt wurde, der Süßigkeitenkonsum an zehn aufeinander folgenden Arbeitstagen festgehalten. In der ursprünglichen Version sind neben Tag und Mitarbeiter Informationen zur Anzahl an gegessenen Obststücken, Gummibärchen und Snickers enthalten. Außerdem gibt die Faktor-Variable „Pick Up“ die Lieblingssorte des Schokoriegels jedes Mitarbeiters. Die Lieblingssorte ist (zumindest über die beobachteten zehn Tage) konstant und verändert sich somit nicht.

Um einen besseren Überblick über den Datensatz vor und nach der Umstrukturierung zu erhalten, werden die Angaben zu Gummibärchen und Snickers entfernt, so dass die Anzahl an gegessenen Obststücken die einzige Information ist, die über die Zeit variiert. In diesem Eintrag wird öfter erwähnt werden, dass eine Variable über die Zeit konstant ist oder variiert. Streng genommen ist der Ausdruck „Zeit“ falsch, denn eine Information kann auch über verschiedene Messhintergründe/Begebenheiten konstant sein oder variieren.

Die ersten fünf Zeilen im Datensatz sind folgend dargestellt:

datenaufbereitung head daten long

Aus der obigen Erklärung wissen wir, dass die Daten momentan noch im Long-Format vorliegen. Jeder Tag wird in einer eigenen Zeile dargestellt, somit kommt jeder Mitarbeiter öfter vor (hier zehn Mal, weil Beobachtungen zu zehn Tagen vorliegen).

Die Umstrukturierung soll also bewirken, dass pro Mitarbeiter nur noch eine Zeile im Datensatz besteht, dafür sollen zehn Informationen zum Obstkonsum vorhanden sein. Da die Pick Up-Vorliebe über die Zeit konstant ist, wird sie nur einmal dargestellt. Ein Nachteil des Long-Formats ist also, dass einige Informationen auch redundant vorhanden sind. Jetzt wird auch klar, warum wir in diesem Eintrag auf die Informationen zum Verzehr von Snickers und Gummibärchen verzichten: Der Datensatz würde sonst so „breit“, dass man ihn nicht mehr übersichtlich darstellen könnte.

So soll der Datensatz dann im Wide-Format aussehen:

datenaufbereitung head daten wide

Durchführung

Um einen Datensatz zu transformieren werden bestimmte Variablen benötigt:

Bei der Umwandlung vom Long- zum Wide-Format wird eine Variable benötigt, die die Messung (zu verschiedenen Zeitpunkten/Begebenheiten) enthält. Diese wird im Folgenden als Measurement (Messung) bezeichnet. Im Süßigkeiten Datensatz ist dies die Anzahl an gegessenen Obststücken. Außerdem muss selbstverständlich eine Variable bestehen, die die Begebenheit der Messung klassifiziert, in unserem Datensatz der Tag. Es kann aber auch einen bestimmten Umstand einer Messung bezeichnen, beim Beispiel aus der Einleitung könnten die Temperaturen beispielsweise auch zur gleichen Zeit aber mit Unterschiedlichen Geräten gemessen werden. Die Variable wird im Folgenden Condition (Bedingung) genannt. Wir werden bei der Anwendung in der Software sehen, das zuweilen auch eine Variable vorhanden sein muss, die die Einheit, in unserem Fall die Mitarbeiter, spezifiziert.

Soll ein Datensatz vom Wide- ins Long-Format transformiert werden, so müssen mindestens zwei Variablen mit dem gleichen Datentyp vorhanden sein. Je nach Software muss außerdem pro Einheit eine konstante Benennung oder die Bezeichnung für die neu zu erstellende Condition-Variable definiert werden.

Wie bereits festgestellt wurde, ist der Datensatz, der bisher verwendet wurde, im Long-Format dargestellt. Um Verwirrung zu vermeiden, wird der Datensatz deshalb als „sweets_long“ bezeichnet. Bei der Durchführung in R, Stata und SPSS wird zunächst gezeigt, wie sich der Datensatz ins Wide-Format umwandeln lässt. Zu Demonstrationszwecken wird er dann erneut ins Long-Format transformiert.

R

Die baseR-Methode zum Reshape von Daten ist die Funktion reshape(). Häufig verwendete Funktionen sind außerdem melt() und cast() aus dem reshape2-Paket sowie gather() und spread() aus dem tidyr-Paket: Der Funktionsaufruf wird hier nur bei den letztgenannten besprochen, da die Funktionen als am intuitivsten gelten.

Der Datensatz, der ja bereits im Long-Format vorliegt, kann mit der spead()– Funktion ins Wide-Format umgewandelt werden. Zunächst muss selbstverständlich der Datensatz definiert werden. Spezifiziert werden müssen außerdem, wie bereits erwähnt, die Measurement- und Condition-Variable. Erstere, in unserem Fall „Obst“, wird an das Argument value übergeben. Die Condition-Variable, die von uns durch „Tag“ dargestellt wird, muss beim Argument key definiert werden.

Nach Ausführung des Befehls erhält man folgendes Resultat:

datenaufbereitung wide R

Wie gewünscht hat der Datensatz nur noch vier Beobachtungen, pro Mitarbeiter jedoch zehn Obst-Variablen, sowie eine PickUp-Variable, die über alle Tage konstant ist. Die neu erstellten Obst-Variablen sind alle mit der Bezeichnung der Tage benannt, es wird hier nicht direkt ersichtlich, dass es sich um die Beobachtungen des Obst-Verzehrs handelt. Optional können die Variablennamen deshalb noch angepasst werden. Der zugehörige Befehl ist in der untenstehenden Codebox zu finden. Dadurch sind die Variablen dann „obst_9“ für den 09.10.2017, „obst_10“ für den 10.10.2017 usw. benannt. Leider ist es mit der grundsätzlichen Funktionalität von spead() lediglich möglich eine zeitvariate Variable umzustrukturieren.

Mit gather() können die Informationen wieder ins Wide-Format gebracht werden. Dafür können dieselben Argumente verwendet werden wie beim Funktionsaufruf von spead(). Zusätzlich müssen hier noch zeitkonstante Variablen definiert werden. Dies sind in unserem Fall die Mitarbeiter und die PickUp-Variable. Die Ausführung des Befehls bringt folgendes Resultat:

datenaufbereitung long R

Da die Measurement-Variablen im Vorhinein umbenannt wurden, ist die Tag-Bezeichnung nun „obst_9“ usw. Um wieder mit einem Datum arbeiten zu können, müssten die Faktorstufen dieser Variable umbenannt und ggf. der Variablentyp angepasst werden (siehe für letztgenanntes auch den Blogeintrag zum Thema Datentypen). Ansonsten ist die Umstrukturierung gelungen und im Kern liegt der gleiche Datensatz vor wie zu Beginn.

## Reshape mittels tidyr: gather & spread 
# Long zu Wide: Spread  
sweets_wide1 <- spread(data = sweets_long, key = tag, value = obst) 

# Umbenennung der Variablen 
names(sweets_wide1)[3:12] <- paste0("obst_", c(9:13, 16:20)) 

# Wide zu Long: Gather 
sweets_long1 <- gather(data = sweets_wide1, key = tag, value = obst, -c(mitarbeiter, pickup))

Stata

Der Befehl reshape führt in Stata die gleichnamige Operation aus. Nach dem Schlagwort „reshape“ muss das Format spezifiziert werden, in das der Datentyp umgewandelt werden soll, also „wide“ oder „long“. In beiden Fällen muss die Measurement-Variable angegeben werden und im Gegensatz zu R auch eine Variable, die die Einheiten eindeutig kennzeichnet, als für den Süßigkeitendatensatz die Mitarbeiter-Variable, in anderen Fällen kann es jedoch auch eine ID sein. Der generelle Aufbau ist reshape format measurement, i(i) j(j), wobei „format“ durch „long“ oder „wide“ spezifiziert wird, measurement die entsprechende Variable, i die eben genannte Indexvariable darstellt und j die Condition angibt.

Dadurch ergibt sich für die Transformation von Long zu Wide der in der Codebox angegebene Befehl. Im Gegensatz zu R können auch mehrere Measurement-Variablen angegeben werden. Da Variablen mit Datumsformat in Stata intern nicht so abgespeichert wird wie es angezeigt wird, wird die Obstvariable für die verschiedenen Tage nicht anhand des angezeigten, sondern des intern gespeicherten Datums bezeichnet. Deshalb können auch hier die Variablennamen noch geändert werden. Führt man den unten dargestellten Befehl aus, so erhalten die Daten im Wide-Format folgendermaßen:

datenaufbereitung wide stata

Aus Platzgründen werden nur die ersten Obst-Variablen dargestellt.

Für den Reshape in die umgekehrte Richtung (Wide zu Long) muss eine Angabe für j nicht zwingend gegeben sein. Hierbei handelt es sich nur um eine Benennung für die zu erstellende Condition-Variable. Als Measurement können entweder mehrere Variable angegeben werden oder, wie bei Stata generell möglich, eine einheitliche Abkürzung aller entsprechenden Variablen. In unserem Fall ist dies der Wortstock „obst“. Der Ausschnitt des so resultierenden Datensatzes zeigt, dass der ursprüngliche Datensatz wiederhergestellt ist:

datenaufbereitung long stata

Benötigt man die Restrukturierung nur temporär und will danach wieder ins ursprüngliche Format zurück, so kann ganz einfach der Befehl reshape long um ins Long- oder reshape wide um ins Wide-Format zurückzukehren, verwendet werden.

*Long zu Wide: 
reshape wide obst, i(mitarbeiter) j(tag) 

*Wide zu Long: 
reshape long obst, i(mitarbeiter) j(tag)

SPSS

In SPSS erfolgt die Transformation mit den Befehlen CASETOVARS bzw. VARSTOCASES, je nachdem, ob Fälle in Variablen umgewandelt werden sollen (Long- zu Wide-Format) oder vice versa.

Beim Reshape von Long zu Wide müssen zwei Variablen definiert werden: die ID-Variable und die Indexvariable. Erstere kennzeichnet die Einheiten, im Beispiel also die Mitarbeitervariable. Die Indexvariable kennzeichnet die unterschiedlichen Zeitpunkte/Messungen/Beobachtungen. Dies ist im Beispiel die Tagesvariable. Sobald diese Sonderzeichen oder beispielsweise Punkte enthält, ist eine logische Benennung der zu erstellenden Variablen nicht mehr möglich und es werden die Namen „v1“ usw. vergeben. Anhand des Labels kann der Ursprung jedoch trotzdem erkannt werden.

Bei der Transformation erkennt SPSS automatisch, welche Variablen zeitkonstant sind und welche über die Zeit variieren und somit umstrukturiert werden müssen. Im Wide-Format resultiert der folgende Datensatz. Es ist zu beachten, dass die Variablennamen hier noch nicht angepasst wurden.

datenaufbereitung wide SPSS

Die Syntax zum Reshape von Wide zu Long ist ebenfalls in der Codebox unten dargestellt. Diese gilt für unser Beispiel, in dem unsere Variablen nur ein Measurement darstellen. Für die Bezeichnung der Tag-Variable wird hier eine Indexierung gewählt, die später noch umgewandelt werden kann, alternativ könnten auch die Variablennamen verwendet werden. Die Indexoption muss dann /INDEX = Index1(obst) lauten.

Auch in SPSS ist es möglich mehrere Variablen umzustrukturieren. Bei der Transformation zum Long-Format können in der Syntax zusätzliche /MAKE-Optionen hinzugefügt werden.

datenaufbereitung long SPSS

*Long zu Wide: 
SORT CASES BY mitarbeiter tag. 
CASESTOVARS 
  /ID=mitarbeiter 
  /INDEX=tag 
  /GROUPBY=VARIABLE. 

*Wide zu Long: 
VARSTOCASES 
  /ID=id 
  /MAKE obst FROM v1 v2 v3 v4 v5 v6 v7 v8 v9 v10 
  /INDEX=tag(10) 
  /KEEP=mitarbeiter pickup 
  /NULL=KEEP.

Zusammenfassung

Der Hintergedanke beim Reshape von Daten ist in R, Stata und SPSS gleich. Die Umsetzung unterscheidet sich jedoch besonders auch im Hinblick auf die Variablen/Informationen, die angegeben werden müssen.
Falls es mal mit der Datenaufbereitung nicht so klappt, helfen wir bei STATWORX gerne dabei, gut in Form zu kommen. Jessica Gerhard Jessica Gerhard

Hauptanalyse

Unsere Archäologen stehen vor ihrem analytischen Ziel, die Voraussetzungsprüfung der ANOVA ist überstanden. Zur Erinnerung noch einmal die Forschungsfrage:

H1: Je länger die Löwen bei den Zirkusspielen im Einsatz sind, desto höher ist ihr Gewicht.

Da alle Daten (Gewicht als metrische und Monate im Zirkus als kategoriale Variable) vorbereitet sind, kann es direkt losgehen. Der Stata-Befehl für die Analyse ist:

anova gewicht monate_kat

und erzeugt die untenstehenden Ergebnisse.

Ergebnisse der ANOVA

Insgesamt liegen N = 517 Fälle für die Analyse vor, der erklärte Varianzanteil beträgt $R^2$ = 0.7505 = 75.05%. Die kategorisierten Monate können also einen sehr hohen Varianzanteil am Gewicht erklären. Darunter folgt eine Zeile für Model und eine Zeile für die Monate. Beide Zeilen sind in diesem einfachen Modell gleich was die Werte angeht (SS steht für Sum of Squares). Für Nutzer von SPSS sei an dieser Stelle gesagt, dass hier nur eine der beiden Zeilen aufgeführt wird und mit „zwischen den Gruppen“ (engl.: between groups) beschriftet ist. Vor allem der englische Begriff ist in der statistischen Fachwelt sehr gebräuchlich und hätte von Stata auch verwendet werden sollen. Die Zeile „residuals“ wird bei SPSS „innerhalb der Gruppen“ (eng.: within groups) genannt, auch hier ist der englische Fachbegriff durchaus in deutscher Fachliteratur üblich.
Zusätzlich findet sich beim between-Effekt die Angabe des F-Werts sowie der dazu gehörende Signifikanzwert. Dieser ist mit $p le .001$ signifikant, so dass die Monate im Zirkus einen signifikanten Effekt auf das Gewicht haben. Eine Aussage darüber, welche Kategorien der Monate hier genau signifikant sind und welchen Unterschied diese bezüglich des Gewichts haben, kann an dieser Stelle noch nicht getroffen werden. Dokumentiert wird das Ergebnis der ANOVA mit F(df1,df2) = F-Wert, p-Wert. In unserem Fall also mit F(5,511) = 311.49, $p le .001$ .
In einigen Fachbereichen ist es üblich die Effektstärke der Analyse mit anzugeben. Ohne auf die Bedeutung dieser Maßzahl näher einzugehen, sei hier kurz gesagt, dass eine Effektstärke eine Aussage darüber trifft, ob ein gefundener Zusammenhang einer Analyse auch eine praktische Relevanz besitzt. Für die ANOVA lässt sich $eta^2$ als Effektstärke einfach berechnen:

$eta^2 = frac{ SS_{between} }{ SS_{top} } = frac{415662.19} {552039.08} = 0.753$

In einer einfaktoriellen Varianzanalyse wie dieser lässt sich $eta^2$ einfach mit 100 multiplizieren, und es gilt:

$R^2 = eta^2$

Somit lässt sich die Interpretation von $eta^2$ ebenso einfach auf den Korrelationskoeffizienten r herunterbrechen, welcher einfach mit

$r = sqrt{R^2} = 0.868$

zu berechnen ist (Field 2013: 472). Auch hier zeigt sich der extrem starke Effekt der ANOVA. Stata kann die Effektstärke auch direkt nach der ANOVA berechnen, dafür muss folgender Befehl verwendet werden

estat esize

Da $eta^2$ mathematisch einen Bias aufweist (Levine 2002), wird meist Omega-Quadrat als Maß der Effektstärke für eine ANOVA angegeben. Stata kann dies mittlerweile von Haus aus berechnen mit

estat esize, omega

Das Ergebnis ist $omega^2 = 0.7502$ , hinsichtlich der Grenzwerte gelten die gleichen wie für $eta^2$ (Kirk 1996). Es liegt also ein starker Effekt vor. Doch wie unterscheiden sich nun die Monate im Detail?

posthoc-Test

Zur Erinnerung wie schwer die Löwen durchschnittlich in den einzelnen Monatskategorien sind, wird die Tabelle aus Teil 2 an dieser Stelle noch einmal gezeigt.

Deskriptive Übersicht

Stata bietet im Nachgang der ANOVA mehrere posthoc Befehle an. Mit

pwcompare monate_kat, group effects mcompare(bon)

würden alle Monatskategorien, d.h. alle möglichen Kombinationen, miteinander verglichen werden. Dies erzeugt eine recht große Tabelle, die hier nicht abgebildet wird, da sie für uns nicht von Interesse ist. Da es das Ziel der Forscher war zu untersuchen, ob mit längerem Aufenthalt die Löwen bei den Zirkusspielen an Gewicht zunehmen, interessiert uns im Moment nur, ob Löwen, die in der nächsthöheren Kategorie von Monaten sind, sich gegenüber der vorherigen Kategorie unterscheiden. Der Befehl „pwcompare“ kann uns hier jedoch nicht weiterhelfen, so dass wir nunmehr

contrast ar.monate_kat, mcompare(bon) effects

durchführen müssen. Mit der Präfix “ar.” weisen wir Stata an, beginnend mit der ersten Kategorie (weniger als 6 Monate) immer zur nächsthöheren Kategorie zu vergleichen. Die Ergebnisse sind in der unten stehenden Tabelle zu finden.

Tabelle posthoc

Die Kategorie „6-10 Monate“ unterscheidet sich von der Kategorie „ $le$ 6 Monate“ um 29.71. Der Kontrast ist dabei nichts anderes als die Differenz der Mittelwerte dieser Kategorien, also 131.17 – 101.46 = 29.71. Dabei wird immer die zuletzt genannte Kategorie des Kontrasts von der zuerst genannten Kategorie abgezogen. Da der Wert positiv ist, bedeutet dies also, dass die Löwen mit 6-10 Monaten im Zirkus durchschnittlich 29,71kg schwerer sind als Löwen die weniger als 6 Monate im Zirkus sind. Dieses Ergebnis ist mit t = 12.97, $p le .001$ signifikant. Als posthoc Test wurde Bonferroni durchgeführt. Eine Diskussion der unzähligen Tests kann an dieser Stelle nicht gegeben werden und es sei an dieser Stelle auf weiterführende Fachliteratur verwiesen (Field 2013: 458 ff.). Auch wenn Bonferroni recht konservativ rechnet, so kann mit Blick auf diese Analyse gesagt werden, dass keine andere Testmethode ein anderes Ergebnis hervorbringt.
Der Blick auf die Tabelle verrät also, dass die Löwen mit zunehmender Zahl an Monaten schwerer werden, zunächst legen sie 29.71kg ( $p le .001$ ) zu, dann 33.41kg ( $p le .001$ ), die Gewichtszunahme verringert sich dann auf 14.91kg ( $p le .001$ ) beim Vergleich von „16-20 Monate“ vs. „11-15 Monate“ und beim darauf folgenden Vergleich liegt die Zunahme lediglich bei durchschnittlich 4.17kg, ist aber mit p = .720 nicht signifikant. Im Vergleich der letzten und vorletzten Kategorie miteinander nehmen die Löwen dann wieder ab, der Kontrast liegt bei -15.15 ( $p le .01$ ).
Mit Hilfe des komfortablen Befehls „margins“ bzw. „marginsplot“ lässt sich nun folgende Grafik zu dieser Veränderung anzeigen, wobei auf den Code, der trotz der Einfachheit der Darstellung relativ lang ist, an dieser Stelle verzichtet werden soll.

Abbildung zu Kontrasten - Gewicht und Monate im Zirkus

Auch wenn die obenstehende Grafik inhaltlich bereits die Wünsche der Forscher erfüllt, soll eine weitere erzeugt werden (siehe unten). Diese Grafik zeigt den Wert des Kontrasts zwischen den aufsteigenden Kategorien der Monate auf. Zusätzlich wurde ein rote Linie am Wert für 0kg abgetragen, welche einmal durch das Konfidenzintervall durchbrochen wird. Bei „21-25 vs. 16-20“ Monate ist der Kontrast +4.17kg, es liegt also noch eine leichte Gewichtszunahme vor, das Konfidenzintervall liegt jedoch zwischen -3.20 und +11.53. Mit einer 95%igen Wahrscheinlichkeit liegt der Kontrast also in diesem Bereich und umschließt den Wert 0. Das Ergebnis ist somit auch ohne den eigentlich p-Werten zu kennen, nicht signifikant, da der Kontrast anstatt positiv (+4.17kg) auch negativ sein kann (bis -3.20kg) und die inhaltliche Interpretation komplett anders wäre.

Abbildung zu Kontrasten - Veränderung von Gewicht und Monaten im Zirkus

Die Forscher sehen ihre Hypothese als größtenteils bestätigt, fragen sich aber nach der ersten Euphorie, ob denn nicht das Alter der Löwen einen Nebeneffekt hat, den man statistisch Kovariate nennt und zu einer Kovarianzanalyse (ANCOVA) führt.

Referenzen

Cohen, J. (1988): Statistical Power Analysis for the Behavioral Sciences. Hoboken: Taylor and Francis
Field, Andy (2013): Discovering Statistics Using SPSS. 4th Edition, SAGE: London
Kirk, R. E. (1996): Practical significance: A concept whose time has come. Educational and Psychological Measurement 56(5), S. 746-759
Levine, T. R., & Hullett, C. R. (2002). Eta Squared, Partial Eta Squared, and Misreporting of Effect Size in Communication Research. Human Communication Research 28(4), S. 612–625

Nick Bornschein Nick Bornschein

Obwohl wir beim letzten Mal nur um Haaresbreite dem Sog des schwarzen Lochs entkommen sind, welches sich in der Nähe der Welt des Wilcoxon-Rangsummen-Tests befindet (Die ganze Geschichte gibt es hier!), lassen wir uns nicht einschüchtern und setzen unsere Entdeckungsreise durch das nicht-parametrische Universum fort.

Den nächsten Planeten, den wir dabei erkunden wollen, könnte man auf den ersten Blick mit der Welt des Wilcoxon-Rangsummen-Tests verwechseln (Lieber daran interessiert? Dann klicke hier.). Beide Welten haben eine ähnliche Flora und Fauna, doch schaut man genau hin, gibt es kleine, aber bedeutende Unterschiede. Acissej, unsere Botanikerin an Bord und im ganzen Universum von den großfüßigen Blaustirnblatthühnchen gefürchtet, kennt sich in diesem Bereich bestens aus. Sie führt daher unsere Expedition zur Erforschung der Welt des Wilcoxon-Vorzeichen-Tests an.

Zwei Welten – Gemeinsamkeiten und Unterschiede

Bei der Erkundung wird als erstes eine Gemeinsamkeit beider Welten deutlich: Der Wilcoxon-Vorzeichen- und der Wilcoxon-Rangsummen-Test sind jeweils die nicht-parametrische Alternative für den t-Test. Ersterer ist das Pendant zum t-Test für abhängige und letzterer zum t-Test für unabhängige Stichproben (Was ist ein t-Test? Hier erfährst du es.). Nicht-parametrisch bedeutet, dass beide Tests weniger strenge Annahmen über die Verteilung der abhängigen Variable machen. Zusätzlich teilen beide die Eigenschaft, dass sie die Mediane von zwei Gruppen auf signifikante Unterschiede testen. Acissej ergänzt noch scherzend, dass sich der Erfinder beider Tests – Frank Wilcoxon – auch in beiden Bezeichnungen verewigt hat.

Bei den vielen Gemeinsamkeiten beider Welten gibt es jedoch einen großen Unterschied zwischen ihnen: Die Situation, in der die Anwendung des Tests angemessen ist. Der Wilcoxon-Vorzeichen-Test wird ausschließlich bei abhängigen Stichproben angewandt. Doch was genau bedeutet Abhängigkeit überhaupt? Häufig bedeutet es, dass bei verschiedenen Personen ein bestimmtes Merkmal zwei Mal gemessen wurde. In diesem Fall spricht man von Messwiederholung. Abhängigkeit kann aber auch bedeuten, dass man die Werte von zwei Person durch eine Gemeinsamkeit in Verbindung bringen kann. Da fällt Acissej sofort ein gutes Beispiel ein: Wenn sich zwei Mitglieder unserer Crew eine Kajüte teilen müssen und der eine schlechte Laune hat, weißt du sofort, wie es dem anderen geht. Ob Sie wollen oder nicht, Ihre Laune ist voneinander abhängig! Bei Abhängigkeiten zwischen Messungen gilt jedoch, dass man nur solche berücksichtigen kann, die eine gewisse Systematik aufweisen⁽¹⁾. Beispielsweise kann die Laune eines Crewmitgliedes die Laune aller Mitglieder am Bord beeinflussen. Da es aber nicht (einfach) zu erfassen ist, wer sich mit wem unterhält und sich dadurch beeinflusst, ist diese eine Form von Abhängigkeit, die man statistisch nicht berücksichtigen würde.

Die Tiefen der Welt des Wilcoxon-Vorzeichen-Tests

Acissej hat heute extrem gute Laune und das perfekte Beispiel parat, um zu erklären, wie die Welt des Wilcoxon-Vorzeichen-Tests im Detail beschaffen ist. Dazu kramt sie einen Zettel aus ihrer Tasche, auf den wir folgendes Lesen können:

Pflanzennummer	Größe beim Einpflanzen [cm]	Größe am nächsten Tag [cm]
1	20,03	21,39
2	20,13	21
3	20,23	21,35
4	20,15	20,75
5	20,46	20,25
6	20,43	20,68
7	20,67	20,53
8	20,35	21,05
9	20,85	20,97
10	20,08	20,62
11	20,5	20,81
12	21,04	20,92
13	20,88	20,95
14	19,94	20,74
15	20,08	20,63

Ihr Beispiel handelt natürlich von Pflanzen. Acissej hat ein kleines Experiment durchgeführt und möchte jetzt wissen, ob es geglückt ist. Sie hat gestern 15 neue Pflanzen in ihrer Kajüte eingepflanzt und gemessen, wie groß diese waren. Zum Einpflanzen hat sie aber nicht herkömmlichen Boden, sondern Kaffeesatz verwendet. Auf diese Idee kam sie als sie vor kurzem auf einer anderen Welt gesehen hat, dass die Einheimischen dort Pflanzen auf den Resten anderer Pflanzen züchten. Da sie als Botanikerin weiß, wie viele Nährstoffe in Kaffee enthalten sind und sie selbst jeden Tag mindestens 10 Tassen trinkt, erschien ihr die Verwendung von Kaffeesatz eine geniale Idee. Heute Morgen hat Sie gleich mal nachgemessen und alles auf dem Zettel notiert. Jetzt möchte sie wissen, ob die Pflanzen im Schnitt gewachsen sind, damit sie sie nicht quält, falls alles eine blöde Idee war.

Da „leider“ nur 15 Pflanzen in ihre Kajüte passen und die Messungen voneinander abhängig sind, empfiehlt sich die Anwendung des Wilcoxon-Vorzeichen-Tests. Dieser bildet zuerst die Differenzen aus beiden Zeitpunkten: Größe beim Einpflanzen – Größe am nächsten Tag (siehe Tabelle 2). Anschließend wird für jede Differenz das Vorzeichen notiert und Ränge vergeben. Bei der Vergabe der Ränge wird das Vorzeichen ignoriert (siehe Tabelle 2).

Pflanzennummer	Differenz	Ränge	Vorzeichen
1	-1,36	15	–
2	-0,87	13	–
3	-1,12	14	–
4	-0,6	10	–
5	0,21	5	+
6	-0,25	6	–
7	0,14	4	+
8	-0,7	11	–
9	-0,12	3	–
10	-0,54	8	–
11	-0,31	7	–
12	0,12	2	+
13	-0,07	1	–
14	-0,8	12	–
15	-0,55	9	–

Die Ränge werden letztlich zu zwei Rangsummen aufsummiert. Eine Rangsumme für Ränge mit positiven (T+) und eine für Ränge mit negativen Vorzeichen (T-). Um zu testen, ob sich die Mediane in beiden Gruppen unterscheiden, verwendet der Test die Rangsumme der positiven Differenzen T+. Diese ist in unserem Fall 11. Für T+ wird der dazugehörige p-Wert anschließend mit einer der beiden folgenden Methoden berechnet. Entweder, indem die Rangsumme an der Anzahl der Personen in der Gruppe relativiert und durch ihren Standardfehler geteilt wird oder, indem der p-Wert exakt berechnet wird, mit Hilfe einer Simulation. Da in den Daten jeder Wert nur einmal vorkommt und die Stichprobe insgesamt kleiner als 40 ist, muss die exakte Methode angewendet werden. Der exakte p-Wert für die Pflanzengrößen ist 0,003 und das Ergebnis daher signifikant. Man kann also davon ausgehen, dass der Median der Pflanzengröße nach einem Tag (20,81) signifikant größer ist als zum Zeitpunkt des Einpflanzens (20,35). Somit sind nicht nur die Pflanzen von Acissei im Schnitt gewachsen, sondern wir können auch davon ausgehen, dass Kaffeesatz bei weiteren Pflanzen geeignet ist, um als Nährboden zu fungieren. Auf diese Freude holt sich Acissej doch erstmal einen Kaffee!

Referenzen

Eid, M., Gollwitzer, M. & Schmitt, M. (2015). Statistik und Forschungsmethoden (4. Überarbeitete und erweiterte Auflage). Weinheim: Beltz. S. 368.
Wilcoxon, F. (1945). Individual comparisons by ranking methods. Biometrics, 1, 80-83.

Alexander Niltop Alexander Niltop

Zwei Welten – Gemeinsamkeiten und Unterschiede

Die Tiefen der Welt des Wilcoxon-Vorzeichen-Tests

Die versteckten Risiken von Black-Box Algorithmen

Prinzipien für vertrauenswürdige KI

Die Black-Box mit Explainable AI Methoden entschlüsseln

Unsere Top 3 XAI Methoden im Überblick

Mit Permutation Feature Importance effizient Einflussfaktoren identifizieren

Mit SHAP Feature Importance komplexe Zusammenhänge aufdecken

Mit Accumulated Local Effects einzelne Variablen in den Fokus nehmen

Mit Explainable AI Methoden Vertrauen aufbauen

Quellen & Informationen:

Einführung

Häufige Herausforderungen

Modellauswahl

Saisonalität

Hierarchische Daten

Cold Start

Recommender Concept

Zusammenfassung

Profitieren auch Sie von unserer Forecasting Expertise!

Grundlagen der Modellbewertung und Kreuzvalidierung

Allgemeine Ansätze zur Modellevaluation

Wiederholte CV und LOOCV

Der Wert von und der Kompromiss zwischen Verzerrung und Varianz

Implementierung der Kreuzvalidierung in

Die altmodische Art: Die -fold Kreuzvalidierung von Hand implementieren

Daten simulieren, Fehlermetrik definieren und festlegen

Aufteilung der Daten

Training und Validierung des Modells

Iterieren durch die Foldings und Berechnen des CV-Fehlers

Fazit

Quellen

Was dem MAPE alles FÄLSCHLICH vorgeworfen wird

Negative Fehler werden stärker bestraft als positive Fehler

Seine WAHREN Schwächen

Tatsächliche Werte gleich Null sind problematisch

Besonders kleine tatsächliche Werte verzerren den MAPE

Der MAPE sagt nur aus, welche Prognose verhältnismäßig besser ist

Zusammenfassung

Bessere Alternativen

Scaled Measures

Scales Errors

SDMAE

Zusammenfassung

Schlechtere Alternativen

SMAPE

Quellen

Einrichtung

Berechnung der Elastizität der Nachfrage

Preis-Optimierung

Indirekte Verfahren

Experimente

Expertenbefragungen

Kundenbefragungen

Datensatz

Durchführung

R

Stata

SPSS

Zusammenfassung

Hauptanalyse

posthoc-Test

Referenzen

Zwei Welten – Gemeinsamkeiten und Unterschiede

Die Tiefen der Welt des Wilcoxon-Vorzeichen-Tests

Referenzen

Zwei Welten – Gemeinsamkeiten und Unterschiede

Die Tiefen der Welt des Wilcoxon-Vorzeichen-Tests

Referenzen

Der Wert von $k$ und der Kompromiss zwischen Verzerrung und Varianz

Die altmodische Art: Die $k$ -fold Kreuzvalidierung von Hand implementieren

Daten simulieren, Fehlermetrik definieren und $k$ festlegen