Wie Deep muss MLP Deep Learning sein?

Wie bereits im ersten Teil unserer Einführungsreihe zu Deep Learning erwähnt, sind neuronale Netze und Deep Learning aktuell ein aktiver Bereich der Machine Learning Forschung. Während die zugrundeliegenden Idee und Konzepte bereits mehrere Jahrzehnte alt sind, ist die Komplexität der Modelle und Architekturen in den letzten Jahren stetig angewachsen. In diesem Blogbeitrag gehen wir der Frage nach, ob durch die Hinzunahme weiterer Hidden Layer im Kontext von Feedforward Netzen, die Modellgüte zwangsläufig verbessert wird oder ob die erhöhte Komplexität des Modells möglicherweise nicht immer von Vorteil ist. Das Praxisbeispiel der S&P 500 Prognose entspricht dem bereits aus Teil 2 der Einführungsreihe bekannten Setting.

Deep Learning – die Bedeutung der Anzahl der Schichten und Neuronen

Das Team um Geoffrey Hinton zeigte 2006 erstmals, dass das Training eines mehrschichtigen neuronalen Netzes möglich ist. Seitdem ist die sogenannte Tiefe eines neuronalen Netzes, d.h. die Anzahl der verwendeten Schichten, ein möglicher Hyperparameter des Modells. Dies bedeutet, dass während der Entwicklung des neuronalen Netzes die prädiktive Güte des Modells auch über unterschiedlich tiefe Netzarchitekturen hin getestet werden sollte. Aus theoretischer Perspektive führt eine Erhöhung der Schichtenzahl zu einer besseren bzw. komplexeren Abstraktionsfähigkeit des Modells, da die Anzahl der berechneten Interaktionen zwischen den Inputs ansteigt. Die strikte Erhöhung der Anzahl von Neuronenschichten kann jedoch auch zu Problemen führen. Einerseits riskiert man mit tiefen Netzarchitekturen ein schnelles Overfitting auf die Trainingsdaten. Dies bedeutet, dass das Modell durch seine erhöhte Kapazität zu schnell spezifische Eigenschaften der Trainingsdaten lernt, die keine Relevanz für eine Generalisierung auf künftige Testdaten haben. Weiterhin führt eine gesteigerte Modellkomplexität auch zu einem komplexeren Szenario im Rahmen der Parameterschätzung des Modells. Alle neuronalen Netze und Deep Learning Modelle werden mittels numerischen Optimierungsmethoden trainiert. Neue Neuronenschichten bedingen neue zu schätzende Parameter, die das Optimierungsproblem herausfordernder gestalten. Somit kann in sehr komplexen Modellarchitekturen möglicherweise keine ausreichend gute Lösung des zugrunde liegenden Optimierungsproblems gefunden werden. Dies wiederum wirkt sich negativ auf die Qualität des Modells aus.

Die Anzahl der Schichten im neuronalen Netz ist nur einer von vielen Hyperparametern, die bei der Gestaltung der Modellarchitektur berücksichtigt werden müssen. Neben der Anzahl der Schichten ist ein weiterer bedeutsamer Aspekt die Anzahl der Neuronen pro Schicht. Trotz intensiver Bemühungen und Forschung in diesem Bereich ist es bis dato nicht gelungen ein allgemeingültiges Konzept bezüglich der Architektur Neuronaler Netze zu finden. Jeff Heaton, ein bekannter Autor mehrerer Einstiegswerke zum Thema Deep Learning gibt in seinen Büchern⁽¹⁾ die folgenden Faustregeln zur Hand:

• Die Anzahl der Neuronen sollte zwischen der Größe der Input und Output Schicht liegen
• Die Anzahl der Neuronen in der ersten Schicht sollte etwa 2/3 der Größe der Input Schicht betragen
• Die Anzahl der Neuronen sollte die doppelte Größe der Input Schicht nicht überschreiten

Diese Ratschläge sind für Deep Learning Einsteiger hilfreich, besitzen jedoch kaum einen Anspruch auf Allgemeingültigkeit. Die Architektur des Netzes muss i.d.R. von Problem zu Problem neu gestaltet werden.

Empirisches Beispiel

Die unten stehenden Abbildung zeigt die Prognosen zweier neuronaler Netze (orange, blau) sowie der Originalwerte (grau). Das blaue Modell verfügt über eine Neuronenschicht, das orangene Modell über vier Schichten. Beide Modelle wurden für 10 Epochen trainiert. Es lässt sich leicht erkennen, dass durch das Hinzufügen weiterer Schichten ein Zuwachs der Modellgüte beobachtet werden kann.

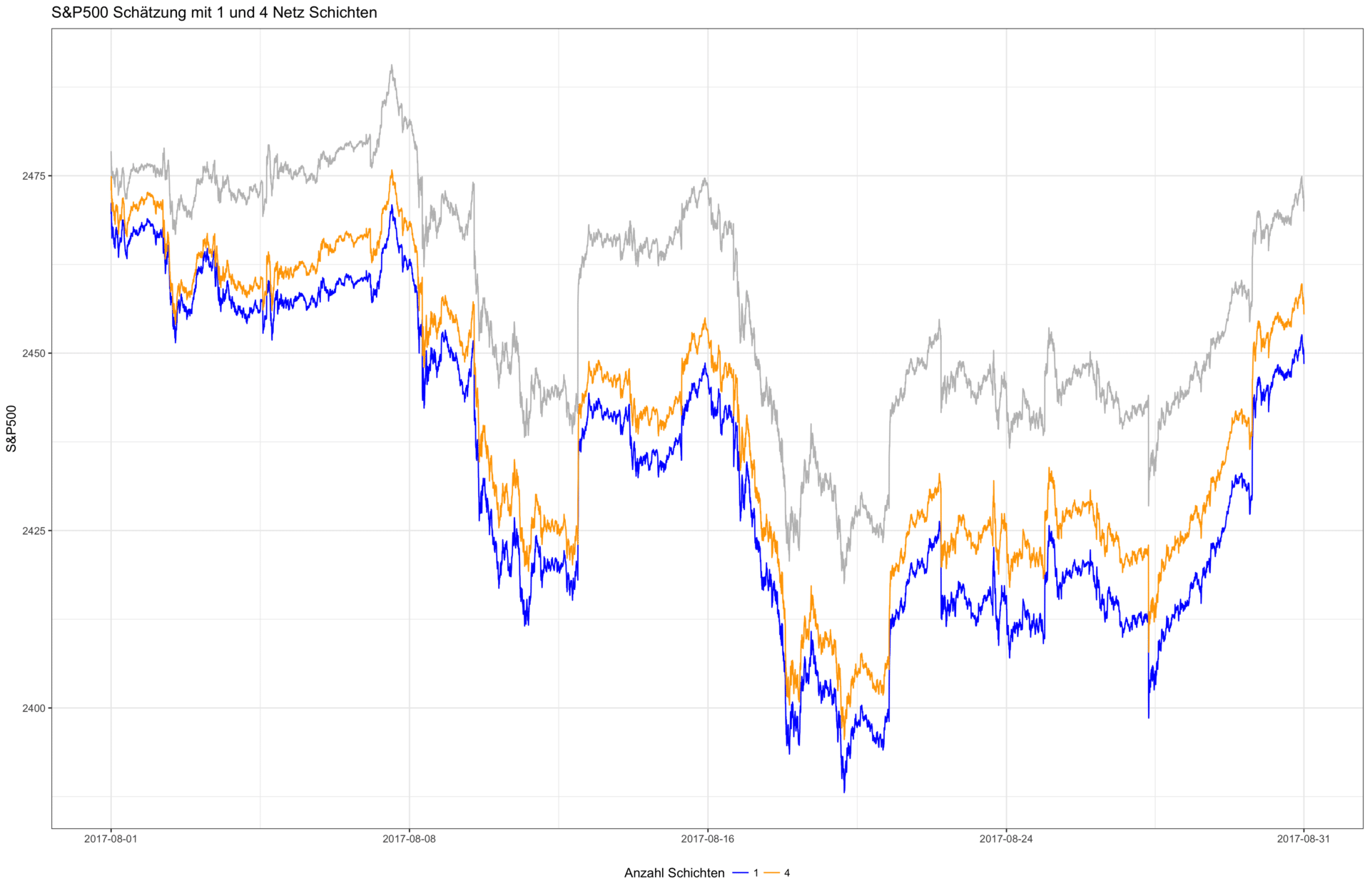
Aufgrund dieses Beispiels sollte jedoch nicht darauf geschlossen werden, dass das Hinzufügen weiterer Schichten immer eine Verbesserung bedingt. Neben dem bereits erwähnten Overfitting-Problem ist es häufig schlichtweg nicht nötig für einfache Probleme ein tief gestaffeltes Netz zu entwerfen. So lässt sich bspw. mathematisch zeigen, dass ein neuronales Netz mit nur einer Schicht und einer endlichen Anzahl an Neuronen jede kontinuierliche Funktion - unter milden Annahmen an die verwendete Aktivierungsfunktion der Neuronen - approximieren kann. Dies nennt man universal approximation theorem.

Im zweiten Experiment untersuchen wir das Zusammenspiel aus Netztiefe und Anzahl der Neuronen. In der unten stehenden Abbildung wurden verschiedene Neuronenkonfigurationen der einzelnen Schichten zusammen mit einer variierenden Netztiefe trainiert. Die Anzahl der Neuronen in der ersten Schicht ist dabei immer abhängig von der Größe der Input Schicht – d.h. der Anzahl der verwendeten Inputs. So weist die Konfiguration "Hälfte des Inputs" für die hier verwendeten 500 Input Faktoren (alle Titel des S&P 500) bspw. die folgenden Neuronenzahl pro Schicht auf – 250, 125, 63, 32, 16. Jede weitere Schicht halbiert in diesem Experiment die Anzahl der Neuronen der vorhergehenden Schicht, um die extrahierten Informationen immer weiter zu verdichten.

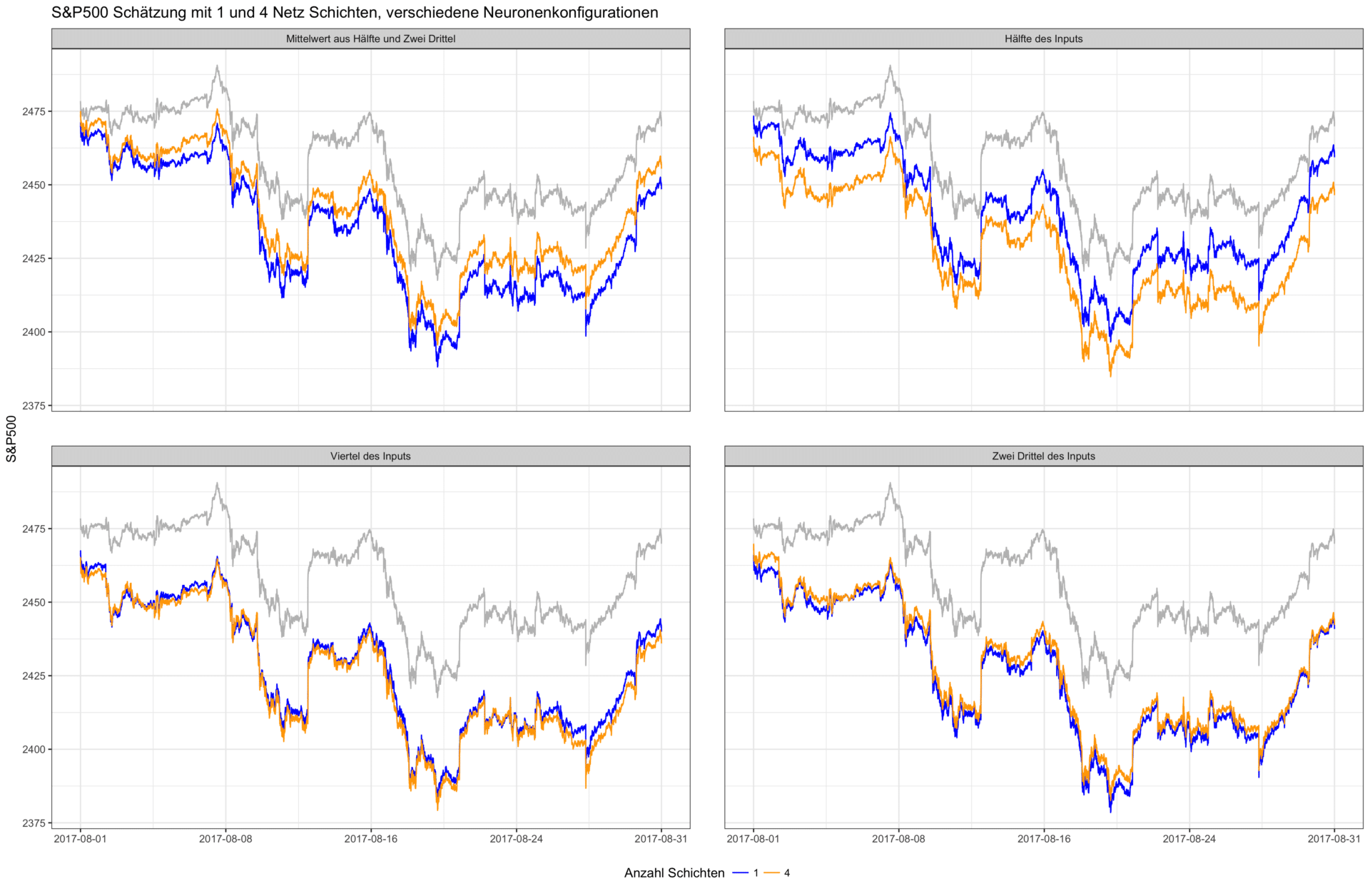
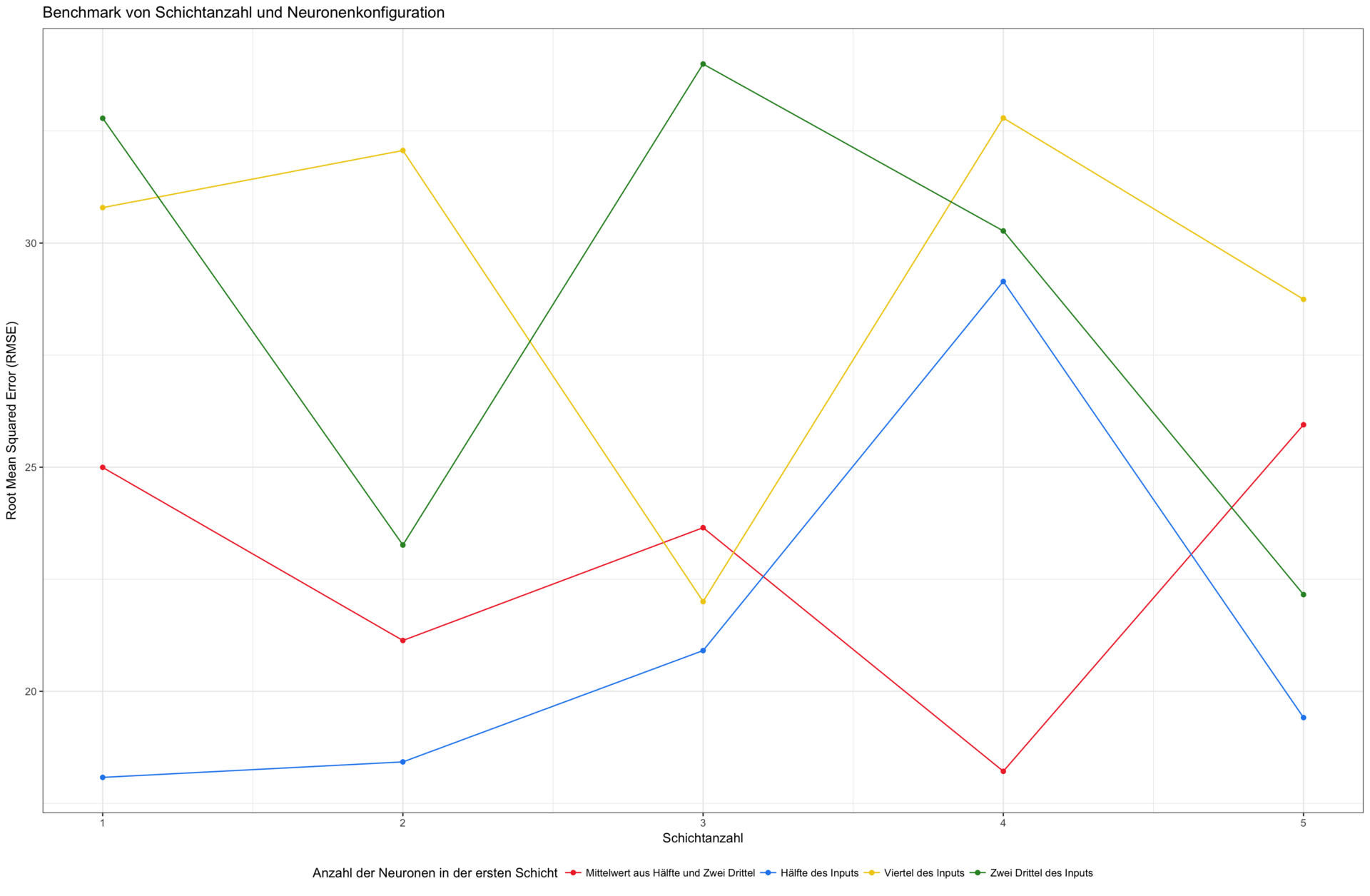
Der Effekt eines tieferen Netzes ist also nicht immer positiv. Besonders deutlich wird dies in der nächsten Grafik. Hier ist der durchschnittliche Vorhersagefehler in Abhängigkeit der gleichen Neuronenkonfigurationen und variierender Netztiefe – von einer bis zu fünf Schichten – abgetragen. Es ist dabei kein generell niedrigerer Fehler bei tieferen Netzen erkennbar.

Ergebnis und Ausblick

Wie lassen sich die Ergebnisse dieses Experiments zusammenfassen? Der wichtigste Punkt ist, dass es selbst für einfache neuronale Netze kein "Standardrezept" gibt. Im Machine Learning Kontext ist dies auch als "no free lunch theorem" bekannt. Weiterhin kann festgehalten werden, dass mehr Schichten nicht zwangsläufig besser sind. Selbst bei einfachen Architekturen sollte man die Anzahl der Schichten sowie die Neuronenkonfiguration als variablen Hyperparameter behandeln und mittels Kreuzvalidierung für die vorliegende Aufgabe optimieren. Hierfür gibt es verschiedene Ansätze, wie z.B. den stückweisen Aufbau eines Netzes bis eine Zielperformance erreicht wird oder das Trimmen großer Netze, bei denen unwichtige Neuronen (solche die nie aktiviert werden) schrittweise entfernt werden. Die Faustregeln von Heaton und Anderen können hierfür als gute Einstiegspunkte dienen, ersetzen aber nicht ein ausgiebiges Modelltuning.

Referenzen

1. Heaton, Jeff (2008): Introduction to Neural Networks for Java