Das Perzeptron war der erste Typus eines künstlichen Neurons und wurde erstmals durch Frank Rosenbaltt in den späten 1950er Jahren vorgestellt. Das Design des Perzeptrons war durch das Neuronen-Modell nach McCulloch und Pitt inspiriert. Während heutzutage andere Typen von Neuronen das Perzeptron ersetzt haben, findet das grundlegende Design des Perzeptrons in modernen neuronalen Netzwerke weiterhin Anwendung.
Das Perzeptron kann zum Erlernen von linear separierbaren Klassifikationen eingesetzt werden. Hierfür rechnet es Inputs ![]() in einen binären Output
in einen binären Output ![]() um. Gewichte
um. Gewichte ![]() beziffern die Wichtigkeit des jeweiligen Inputs für den Output. Der Output errechnet sich als die gewichtete Summe über die Inputs:
beziffern die Wichtigkeit des jeweiligen Inputs für den Output. Der Output errechnet sich als die gewichtete Summe über die Inputs:
![]()
Schematische Darstellung des Perzeptrons
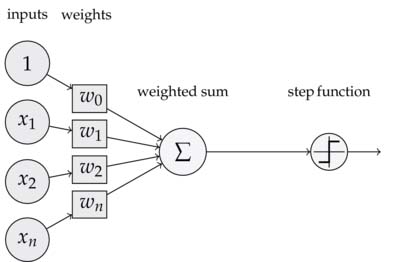
Um sicherzustellen, dass ![]() ein binärer Outcome ist, nutzt das Perzeptron eine Treppenfunktion (auch hard limiter genannt) mit einem geschätzten Schwellenwert, welcher auch Bias genannt wird (in der obenstehenden Abbildung als das Unit-Input dargestellt):
ein binärer Outcome ist, nutzt das Perzeptron eine Treppenfunktion (auch hard limiter genannt) mit einem geschätzten Schwellenwert, welcher auch Bias genannt wird (in der obenstehenden Abbildung als das Unit-Input dargestellt):
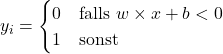
Dabei ist ![]() das Skalarprodukt von
das Skalarprodukt von ![]() und
und ![]() mit dem Bias
mit dem Bias ![]() . Eine Treppenfunktion ist eine nicht-lineare Funktion, welche die gewichtete Summe auf den gewünschten Wertebereich des Outputs abbildet. Eine Bemerkung am Rande: Auch moderne neuronale Netzwerke benötigen eine nicht-lineare Funktion – deren Form ist im Vergleich zur Treppenfunktion jedoch etwas glatter (und wird daher oft soft limiter genannt).
. Eine Treppenfunktion ist eine nicht-lineare Funktion, welche die gewichtete Summe auf den gewünschten Wertebereich des Outputs abbildet. Eine Bemerkung am Rande: Auch moderne neuronale Netzwerke benötigen eine nicht-lineare Funktion – deren Form ist im Vergleich zur Treppenfunktion jedoch etwas glatter (und wird daher oft soft limiter genannt).
Beispiel einer Treppenfunktion
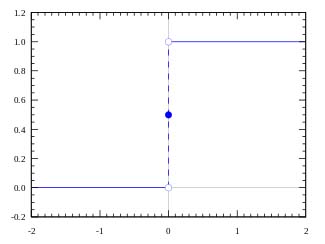
Das Perzeptron lernt durch das iterative Anpassen des Gewichtungsvektors ![]() . Dies geschieht wie folgt:
. Dies geschieht wie folgt:
![]()
Dabei ist ![]() der bisherige Gewichtungsvektors,
der bisherige Gewichtungsvektors, ![]() die Lernrate, und
die Lernrate, und ![]() der Fehler innerhalb der aktuellen Iteration
der Fehler innerhalb der aktuellen Iteration ![]() bezeichnet das aktuelle Input. Die Anpassung der Gewichte erfolgt daher durch den mit dem bisherigen Fehler und der Lernrate gewichteten Input. Dies wird als Perzeptron-Lernregel bezeichnet.
bezeichnet das aktuelle Input. Die Anpassung der Gewichte erfolgt daher durch den mit dem bisherigen Fehler und der Lernrate gewichteten Input. Dies wird als Perzeptron-Lernregel bezeichnet.
Der nachstehende Python-Code illustriert den Mechanismus des Perzeptron-Lernens für das nachstehende, simple Problem:
Gegeben sind die Datenpunkte ![]() und der Vektor
und der Vektor ![]() . der zugehörigen Outputs. Außerdem soll gelten
. der zugehörigen Outputs. Außerdem soll gelten ![]() falls
falls ![]() oder
oder ![]() und
und ![]() anderenfalls.
anderenfalls.
# Coden des Rosenblatt Perzeptrons
# ----------------------------------------------------------
import numpy as np
import random
random.seed(1)
# Treppenfunktion
def unit_step(x):
if x {} | {}".format('Index', 'Probability', 'Prediction', 'Target'))
print('---')
for index, x in enumerate(X):
y_hat = np.dot(x, w)
print("{}: {} -> {} | {}".format(index, round(y_hat, 3),
unit_step(y_hat), y[index]))
%matplotlib inline
import matplotlib.pyplot as plt
# Grafik Trainingsfehler
plt.plot(range(n),errors)
plt.xlabel('Epoche')
plt.ylabel('Fehler')
plt.title('Trainingsfehler')
plt.show() 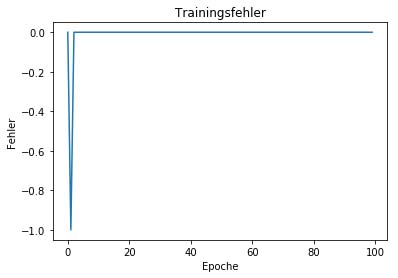
Inputs, vorhergesagte Wahrscheinlichkeiten und Outputs
| Index: | Wahrscheinlichkeit | Vorhersage | Target |
|---|---|---|---|
| 0 | -0.033 | 0 | 0 |
| 1 | 0.382 | 1 | 1 |
| 2 | 0.521 | 1 | 1 |
| 3 | 0.936 | 1 | 1 |
Nach einigen hunderten Iterationen hat das Perzeptron die Gewichte so angepasst, dass alle Datenpunkte korrekt vorhergesagt werden. So ist das Perzeptron in der Lage, unser einfaches Klassifikationsproblem zu lösen. Wie aus der Grafik ersichtlich, sind 100 Epochen dabei mehr als genug und wir hätten den Lernprozess auch früher beenden können.
Wichtig ist hier zu beachten, dass es sich um eine reine In-sample Klassifikation handelt. Das berüchtigte Auswendiglernen (Overfitting) der Trainingsdaten spielt daher keine Rolle. In realen Problemstellungen wird Overfitting zum Beispiel dadurch verhindert, dass der Lernprozess bereits früher abgebrochen wird (das sogenannte Early-Stopping).
Kurz nach seiner Publikation in den frühen 1960er Jahren, erregte das Perzeptron große Aufmerksamkeit und wurde allgemein als leistungsfähiger Lernalgorithmus angesehen. Diese Einschätzung änderte sich durch die berühmte Kritik von Minsky und Papert (1969) in den späten 1960er und frühen 1970er Jahren dramatisch.
Minsky and Papert bewiesen, dass das Perzeptron in dem, was es lernen kann, sehr eingeschränkt ist. Genauer zeigten sie, dass das Perzeptron die richtigen Features benötigt, um eine Klassifikationsaufgabe korrekt zu erlernen. Mit genug handverlesenen Features ist die Performanz des Perzeptrons äußerst gut. Ohne handverlesene Features verliert es jedoch unmittelbar an Lernvermögen.
Yudkowsky (2008 S. 15f.)(3) beschreibt ein Beispiel für das Versagen des Perzeptron aus den Anfangszeiten der neuronalen Netzwerke:
„Once upon a time, the US Army wanted to use neural networks to automatically detect camouflaged enemy tanks. The researchers trained a neural net on 50 photos of camouflaged tanks in trees, and 50 photos of trees without tanks. Using standard techniques for supervised learning, the researchers trained the neural network to a weighting that correctly loaded the training set—output “yes” for the 50 photos of camouflaged tanks, and output “no” for the 50 photos of forest. This did not ensure, or even imply, that new examples would be classified correctly.“
The neural network might have “learned” 100 special cases that would not generalize to any new problem. Wisely, the researchers had originally taken 200 photos, 100 photos of tanks and 100 photos of trees. They had used only 50 of each for the training set. The researchers ran the neural network on the remaining 100 photos, and without further training the neural network classified all remaining photos correctly. Success confirmed! The researchers handed the finished work to the Pentagon, which soon handed it back, complaining that in their own tests the neural network did no better than chance at discriminating photos.
It turned out that in the researchers’ dataset, photos of camouflaged tanks had been taken on cloudy days, while photos of plain forest had been taken on sunny days. The neural network had learned to distinguish cloudy days from sunny days, instead of distinguishing camouflaged tanks from empty forest.“
Unser vorheriges Beispiel, in welchem das Perzeptron ausgehend von dem Input ![]() erfolgreich gelernt, hat den Output
erfolgreich gelernt, hat den Output ![]() korrekt zu klassifizieren, kann als logische ODER-Funktion verstanden werden
korrekt zu klassifizieren, kann als logische ODER-Funktion verstanden werden ![]() falls
falls ![]() oder
oder ![]() . Bei diesem Problem ist ODER als nicht exklusiv definiert.
. Bei diesem Problem ist ODER als nicht exklusiv definiert.
Durch die folgende Abänderung, lässt sich das Problem in eine exklusive XODER-Funktion umgewandelt werden: ![]()
Es stellt sich die Frage, ob das Perzeptron immer noch in der Lage ist, diese neue Funktion korrekt zu approximieren?
random.seed(1)
# Dieselben Daten
X = np.array([[0,0],
[0,1],
[1,0],
[1,1]])
# Zurücksetzen der Vektoren für Gewichte und Fehler
w = np.random.rand(2)
errors = []
# Aktualisieren der Outputs
y = np.array([0,1,1,0])
# Nochmals: Training ...
for i in range(n):
# Zeilenindex
index = random.randint(0,3)
# Minibatch
x_batch = X[index,:]
y_batch = y[index]
# Aktivierung berechnen
y_hat = unit_step(np.dot(w, x_batch))
# Fehler berechnen und abspeichern
error = y_batch - y_hat
errors.append(error)
# Gewichte anpassen
w += eta * error * x_batch
# ... und Vorhersage
for index, x in enumerate(X):
y_hat = np.dot(x, w)
print("{}: {} -> {} | {}".format(index, round(y_hat, 3), unit_step(y_hat), y[index]))
%matplotlib inline
import matplotlib.pyplot as plt
# Grafik Trainingsfehler
plt.plot(range(n),errors)
plt.xlabel('Epoche')
plt.ylabel('Fehler')
plt.title('Trainingsfehler')
plt.show() 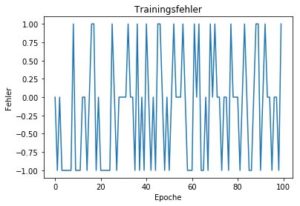
Inputs, vorhergesagte Wahrscheinlichkeiten und Outputs
| Index: | Vorhersage | Target | |
|---|---|---|---|
| 0 | 0.000 | 1 | 0 |
| 1 | 0.024 | 1 | 1 |
| 2 | 0.156 | 1 | 1 |
| 3 | 0.180 | 1 | 1 |
Die Eigenheiten des veränderten Problems machen es dem Perzeptron schwer, die Aufgabe, gegeben der ausgewählten Inputs, korrekt zu erlernen. Wie von Minsky und Papert erörtert, sind die Features der Schlüssel zur Lösung des Problems durch das Perzeptron.
Fazit
Unglücklicherweise, wurde die Kritik von Minsky und Papert von einem großen Teil der Wissenschaftsgemeinschaft missverstanden: Wenn das Lernen der richtigen Features essentiell ist und neuronale Netzwerke allein nicht in der Lage sind, diese Features zu lernen, sind sie nutzlos für alle nicht-triviale Lernaufgaben. Diese Deutungsweise hielt sich für die nächsten 20 Jahre als weithin geteilter Konsens und führte zu einer dramatischen Verringerung des wissenschaftlichen Interesses an neuronalen Netzwerken als Lernalgorithmen.
Als weitere Konsequenz der Erkenntnisse von Minsky und Papert traten zwischenzeitlich andere Lernalgorithmen an die Stelle neuronaler Netze. Einer der prominentesten Algorithmen war die Support Vector Machine (SVM). Durch die Transformation des Input-Raums in einen nicht-linearen Feature-Raum, löste die SVM das Problem an denen neuronale Netzwerke scheinbar scheiterten.
Erst in den späten 1980er und frühen 1990er Jahren gelangte man langsam zu der Erkenntnis, dass neuronale Netze durchaus dazu fähig waren, nützliche, nicht-lineare Features aus Daten zu lernen. Möglich wurde dies durch die Aneinanderreihung mehrerer Schichten von Neuronen. Dabei lernt jede Schicht aus den Outputs der vorhergegangenen. Dies erlaubt das Ableiten von nützlichen Features aus den ursprünglichen Input Daten – also genau die Problemstellung die ein einzelnes Pezeptron nicht lösen kann.
Auch wenn heutiges Deep Learning (also Neuronale Netze mit vielen Schichten) deutlich komplexer ist als das ursprüngliche Perzeptron, baut es doch auf den Grundtechniken dessen auf.
Referenzen
1. Rosenblatt, F. (1958). The perceptron: A probabilistic model for information storage and organization in the brain. Psychological review, 65(6), 386.
2. Minsky, M. L., & Papert, S. A. (1987). Perceptrons-Expanded Edition: An Introduction to Computational Geometry.
3. Yudkowsky, E. (2008). Artificial intelligence as a positive and negative factor in global risk. Global catastrophic risks, 1(303), 184.
