Einer der am häufigsten verwendeten statistischen Tests ist der t-Test. Er kann unter anderem dazu genutzt werden, zu prüfen, ob der Mittelwert einer Zufallsvariable einem bestimmten Wert entspricht. Auch kann er für den Vergleich zweier Mittelwerte herangezogen werden. Wie bei jedem anderen statistischen Test auch, müssen gewisse Voraussetzungen erfüllt sein, damit der t-Test sicher eingesetzt werden kann:
- Normalverteilung der Zufallsvariablen
- Unabhängigkeit der Beobachtungen
- Varianzhomogenität (im Zwei-Gruppenfall)
Wenn diese Voraussetzungen nicht erfüllt sind, ist dennoch nicht aller Tage Abend! Die Robustheit des t-Testes lässt es zu, dass bei größeren Stichprobenumfängen die Normalverteilung weniger wichtig wird(1) . Bei kleinen Stichproben gibt es nicht-parametrische Alternativen, wie den Wilcoxon-Rangsummen-Test. Eine Beschreibung zu diesem Test gibt es hier.
Formeln für unterschiedliche Fälle
Wo genau spielt die Unabhängigkeit eine Rolle? Hierfür ist es wichtig zwischen verschiedenen Fällen zu unterscheiden. Hat man nur eine Variable, so bezieht sich die Unabhängigkeit auf die einzelnen Beobachtungen untereinander. Wenn zwei Zufallsvariablen verglichen werden, dann können folgende Fälle vorliegen, die zu verschiedenen Berechnungen der Teststatistik führen:
| Stichprobe | ||||
|---|---|---|---|---|
| Gepaart / verbunden | Ungepaart / unabhängig | |||
| Varianzen | bekannt | |||
| unbekannt | gleich | |||
| ungleich | ||||
Hierbei stehen
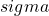 für die Varianz
für die Varianz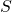 für die geschätzen Varianzen
für die geschätzen Varianzen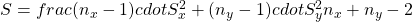
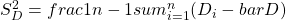
Zum Überprüfen der Voraussetzungen sollte neben weiteren statistischen Tests auch der inhaltliche Aspekt der Variablen genutzt werden. So kann die Frage, ob es sich um eine gepaarte Stichprobe handelt, schon durch die Betrachtung der Untersuchungsmethodik geklärt werden. Wurde zum Beispiel eine Gruppe vor und nach einer Behandlung untersucht, so handelt es sich um eine gepaarte (auch verbunden genannte) Stichprobe.
Wenn die Voraussetzungen geprüft und der t-Test durchgeführt wurden, steht die eigentliche Interpretation der Ergebnisse an. Was genau bedeuten die Zahlen? Welche Schlüsse können gezogen werden? Ist das Ergebnis signifikant? Mit einem kleinen Beispiel sollen diese Fragen geklärt werden.
Beispiel für SPSS Ausgaben
Wir haben insgesamt 400 Beobachtungen simuliert – sagen wir es handelt sich um die Schlafdauer in Stunden. Wir nehmen folgende drei Szenarien an:
- alle Daten stammen von einer Gruppe (Test bei einer Stichprobe)
- die Daten stammen von einer Gruppe in einem Vorher-Nachher-Vergleich (Test bei gepaarten Stichproben)
- die Daten stammen von zwei verschiedenen Gruppen (Test bei unabhängigen Stichproben)
In SPSS gibt es für den t-Test genau diese drei Fälle: bei einer Stichprobe, bei unabhängigen und bei verbundenen Stichproben. Der Output unterscheidet sich leicht, wie in den Abbildungen zu erkennen ist. Dennoch sind die wesentlichen Interpretationen dieselben.

SPSS Ausgabe beim Einstichprobentest

SPSS Ausgabe beim Zweistichprobentest bei abhängigen Stichproben

SPSS Ausgabe beim Zweistichprobentest bei unabhängigen Stichproben
Folgende Werte sind immer gegeben:
- der Wert der Teststatistik „T“
- die Anzahl der Freiheitsgrade „df“ (degree of freedom)
- der p-Wert „Sig. (2-seitig)“
- die „Untere“ und „Obere“ Grenze des Konfidenzintervalls
- der „Mittelwert“ bzw. die „Mittlere Differenz“
Diese Kennzahlen hängen stark miteinander zusammen. So wird der p-Wert mittels dem Wert der Teststatistik und dem Freiheitsgrad bestimmt. Die Grenzen des Konfidenzintervalls sind eine andere Darstellung dafür, ob ein Test signifikant ist oder nicht. Sie enthalten die selbe Aussagekraft wie der p-Wert. Der „Mittelwert“ bzw. die „Mittlere Differenz“ gibt die Abweichung der Daten entweder zum Mittelwert oder unter den Gruppen an. Er hilft, die Aussage des t-Tests in Relation zur Fragestellung zu bringen: Welche Gruppe ist größer? In welche Richtung zeigt der Effekt?
Die Ausgabe des t-Test bei unabhängigen Stichproben enthält zudem noch den Levene-Test. Dieser dient zum Überprüfen der Varianzgleichheit (![]() ). Je nachdem ob hier eine Signifikanz vorliegt, muss die entsprechende Zeile der Tabelle für die Auswertung genutzt werden. Die Werte der beiden Zeilen können sich unterscheiden, was auf die zuvor erwähnten, unterschiedlichen Formeln zurückzuführen ist.
). Je nachdem ob hier eine Signifikanz vorliegt, muss die entsprechende Zeile der Tabelle für die Auswertung genutzt werden. Die Werte der beiden Zeilen können sich unterscheiden, was auf die zuvor erwähnten, unterschiedlichen Formeln zurückzuführen ist.
Auswertung
Was heißt das nun für unser Beispiel? Wie zu erkennen ist, sind die Kennzahlen bei den drei Tests verschieden.
Szenario – Test bei einer Stichprobe
Es gibt hier keinen signifikanten Hinweis darauf, dass der Mittelwert nicht 4,2 in den gesamten Daten ist.
Szenario – Test bei gepaarten Stichproben
Der Unterschied zwischen Vorher und Nachher ist ganz knapp nicht signifikant für ![]()
Szenario – Test bei unabhängigen Stichproben
Es zeigt sich, dass von Varianzhomogenität ausgegangen werden kann und es einen für ![]() signifikanten Unterschied in den Gruppen gibt.
signifikanten Unterschied in den Gruppen gibt.
Zusammenfassung
Die verschiedenen t-Tests können durch Unterschiede in der Berechnung auch unterschiedliche Ergebnisse liefern. Die kann im Extremfall – wie in unserem Beispiel – auch die Signifikanz beeinflussen. Es ist also wichtig sich im Vorfeld darüber klar zu werden, welche Struktur die Daten haben, die man untersucht.
Referenzen
- Eid, Gollwitzer, Schmitt (2015) Statistik und Forschungsmethoden, Kapitel: 12.1, S. 369ff
