Der Vergleich von Prognosemethoden und Modellen über verschiedene Zeitreihen hinweg ist oft problematisch. Dieser Herausforderung sehen wir uns bei STATWORX regelmäßig gegenüber. Einheitenabhängige Maße wie der MAE (Mean Absolute Error) und der RMSE (Root Mean Squared Error) erweisen sich als ungeeignet und wenig hilfreich, wenn die Zeitreihen in unterschiedlichen Einheiten gemessen werden. Ist dies jedoch nicht der Fall, liefern beide Maße wertvolle Informationen. Der MAE ist gut interpretierbar, da er die durchschnittliche absolute Abweichung von den tatsächlichen Werten angibt. Der RMSE hingegen ist nicht so einfach zu interpretieren und anfälliger für Extremwerte, wird aber in der Praxis dennoch häufig verwendet.
![]()
![]()
Eine der am häufigsten verwendeten Messgrößen, die dieses Problem vermeidet, heißt MAPE (Mean Absolute Percentage Error). Er löst das Problem der genannten Ansätze, da er nicht von der Einheit der Zeitreihe abhängt. Außerdem können Entscheidungsträger ohne statistisches Hintergrundwissen dieses Maß leicht interpretieren und verstehen. Trotz seiner Beliebtheit wurde und wird der MAPE immer noch kritisiert.
![]()
In diesem Artikel bewerte ich diese kritischen Argumente und zeige, dass zumindest einige von ihnen höchst fragwürdig sind. Im zweiten Teil meines Artikels konzentriere ich mich auf die wahren Schwächen des MAPE. Im dritten Teil diskutiere ich verschiedene Alternativen und fasse zusammen, unter welchen Umständen die Verwendung des MAPE sinnvoll erscheint (und wann nicht).
Was dem MAPE alles FÄLSCHLICH vorgeworfen wird
Negative Fehler werden stärker bestraft als positive Fehler
Die meisten Quellen, die sich mit dem MAPE beschäftigen, weisen auf dieses „große“ Problem der Messung hin. Diese Aussage basiert hauptsächlich auf zwei verschiedenen Argumenten. Erstens wird behauptet, dass der Austausch des tatsächlichen Wertes mit dem prognostizierten Wert die Richtigkeit der Aussage beweist (Makridakis 1993).
Fall 1: ![]() = 150 &
= 150 & ![]() = 100 (positive error)
= 100 (positive error)
![]()
Fall 2: ![]() = 100 &
= 100 & ![]() = 150 (negative error)
= 150 (negative error)
![]()
Es stimmt, dass Fall 1 (positiver Fehler von 50) mit einem niedrigeren APE (Absolute Percentage Error) verbunden ist als Fall 2 (negativer Fehler von 50). Der Grund dafür ist jedoch nicht, dass der Fehler positiv oder negativ ist, sondern einfach, dass sich der tatsächliche Wert ändert. Wenn der tatsächliche Wert konstant bleibt, ist der APE für beide Fehlerarten gleich *(Goodwin & Lawton 1999)*. Das wird durch das folgende Beispiel verdeutlicht.
Fall 3: ![]() = 100 &
= 100 & ![]() = 50
= 50
![]()
Fall 4: ![]() = 100 &
= 100 & ![]() = 150
= 150
![]()
The second, equally invalid argument supporting the asymmetry of the MAPE arises from the assumption about the predicted data. As the MAPE is mainly suited to be used to evaluate predictions on a ratio scale, the MAPE is bounded on the lower side by an error of 100% (Armstrong & Collopy 1992). However, this does not imply that the MAPE overweights or underweights some types of errors, but that these errors are not possible.
Seine WAHREN Schwächen
Tatsächliche Werte gleich Null sind problematisch
Diese Aussage ist ein bekanntes Problem des Maßes. Dieses und das letztgenannte Argument waren der Grund für die Entwicklung einer modifizierten Form des MAPE, des SMAPE („Symmetric“ Mean Absolute Percentage). Ironischerweise leidet diese modifizierte Form im Gegensatz zum ursprünglichen MAPE unter einer echten Asymmetrie (Goodwin & Lawton 1999). Ich werde dieses Argument im letzten Abschnitt des Artikels erläutern.
Besonders kleine tatsächliche Werte verzerren den MAPE
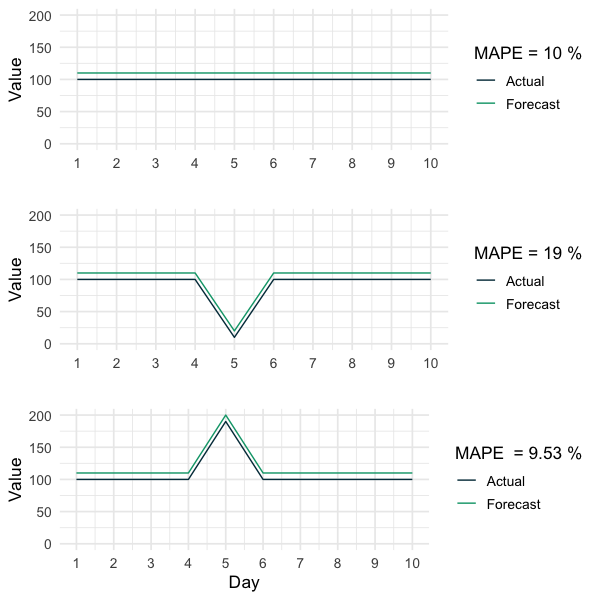
Wenn ein wahrer Wert sehr nahe bei Null liegt, sind die entsprechenden absoluten prozentualen Fehler extrem hoch und verzerren daher die Aussagekraft des MAPE (Hyndman & Koehler 2006). Die folgende Grafik verdeutlicht diesen Punkt. Obwohl alle drei Prognosen die gleichen absoluten Fehler aufweisen, ist der MAPE der Zeitreihe mit nur einem extrem kleinen Wert etwa doppelt so hoch wie der MAPE der anderen Prognosen. Dieser Sachverhalt impliziert, dass der MAPE bei extrem kleinen Beobachtungen vorsichtig verwendet werden sollte und motiviert direkt die letzte und oft ignorierte Schwäche des MAPE.
Der MAPE sagt nur aus, welche Prognose verhältnismäßig besser ist
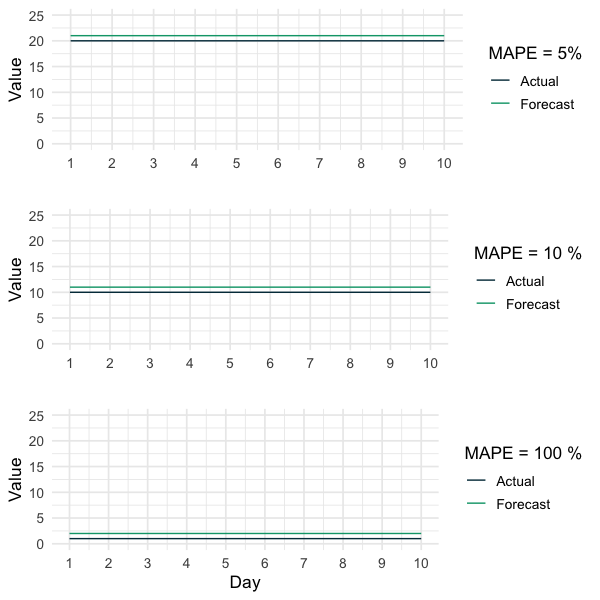
Wie bereits zu Beginn dieses Artikels erwähnt, liegt ein Vorteil der Verwendung des MAPE für den Vergleich zwischen Prognosen verschiedener Zeitreihen in seiner Unabhängigkeit von der Einheit. Es ist jedoch wichtig zu bedenken, dass der MAPE nur angibt, welche Prognose proportional besser ist. Die folgende Grafik zeigt drei verschiedene Zeitreihen und die dazugehörigen Prognosen. Der einzige Unterschied zwischen ihnen ist ihr allgemeines Niveau. Dieselben absoluten Fehler führen also zu völlig unterschiedlichen MAPEs. In diesem Artikel wird kritisch hinterfragt, ob es sinnvoll ist, ein solches prozentuales Maß für den Vergleich zwischen Prognosen für verschiedene Zeitreihen zu verwenden. Wenn sich die verschiedenen Zeitreihen nicht auf einer irgendwie vergleichbaren Ebene verhalten (wie in der folgenden Grafik dargestellt), beruht die Verwendung des MAPE, um zu ermitteln, ob eine Prognose für eine Zeitreihe allgemein besser ist als für eine andere, auf der Annahme, dass dieselben absoluten Fehler für Zeitreihen auf höheren Ebenen weniger problematisch sind als für Zeitreihen auf niedrigeren Ebenen:
„Wenn eine Zeitreihe um 100 schwankt, dann ist die Vorhersage von 101 viel besser als die Vorhersage von 2 für eine Zeitreihe, die um 1 schwankt.“
Das mag in manchen Fällen stimmen. Im Allgemeinen ist dies jedoch eine Annahme, der man sich immer bewusst sein sollte, wenn man den MAPE-Wert zum Vergleich von Prognosen zwischen verschiedenen Zeitreihen verwendet.
Zusammenfassung
Insgesamt zeigen die diskutierten Ergebnisse, dass der MAPE mit Vorsicht als Instrument für den Vergleich von Prognosen zwischen verschiedenen Zeitreihen verwendet werden sollte. Eine notwendige Bedingung ist, dass die Zeitreihe nur streng positive Werte enthält. Zweitens haben nur einige extrem kleine Werte das Potenzial, den MAPE stark zu verzerren. Und schließlich hängt der MAPE systematisch von dem Level der Zeitreihe ab, da es sich um einen prozentualen Fehler handelt. In diesem Artikel wird kritisch hinterfragt, ob es sinnvoll ist, von einer proportional besseren Prognose auf eine allgemein bessere Prognose zu verallgemeinern.
Bessere Alternativen
Die Diskussion zeigt, dass der MAPE allein oft nicht sehr nützlich ist, wenn es darum geht, die Genauigkeit verschiedener Prognosen für unterschiedliche Zeitreihen zu vergleichen. Obwohl es bequem sein kann, sich auf ein leicht verständliches Maß zu verlassen, birgt es ein hohes Risiko für irreführende Schlussfolgerungen. Im Allgemeinen ist es immer empfehlenswert, verschiedene Messwerte kombiniert zu verwenden. Zusätzlich zu den numerischen Messwerten liefert eine Visualisierung der Zeitreihe, einschließlich der tatsächlichen und der prognostizierten Werte, immer wertvolle Informationen. Wenn ein einzelnes numerisches Maß jedoch die einzige Option ist, gibt es einige erwähnenswerte Alternativen.
Scaled Measures
Scaled Measures vergleichen das Maß einer Prognose, z.B. den MAE im Verhältnis zum MAE einer Benchmark-Methode. Ähnliche Maße können mit RMSE, MAPE oder anderen Maßen definiert werden. Gängige Benchmark-Methoden sind der „random walk“, die „naive“ Methode und die „mean“ Methode. Diese Scaled Measures sind leicht zu interpretieren, da sie zeigen, wie das Schwerpunktmodell im Vergleich zu den Benchmark-Methoden abschneidet. Es ist jedoch wichtig zu bedenken, dass sie von der Auswahl der Benchmark-Methode abhängen und davon, wie gut die Zeitreihe mit der gewählten Methode vorhergesagt werden kann.
![]()
Scales Errors
Scaled Errors versuchen ebenfalls, die Skalierung der Daten zu beseitigen, indem sie die prognostizierten Werte mit denen einer Benchmark-Prognosemethode, wie der naiven Methode, vergleichen. Der MASE (Mean Absolute Scaled Error), der von *Hydnmann & Koehler 2006* vorgeschlagen wurde, ist je nach Saisonalität der Zeitreihe leicht unterschiedlich definiert. Im einfachen Fall einer nicht saisonalen Zeitreihe wird der Fehler der Prognose auf der Grundlage des In-Sample-MASE der naiven Prognosemethode skaliert. Ein großer Vorteil ist, dass sie mit tatsächlichen Werten von Null umgehen kann und durch sehr extreme Werte nicht verzerrt wird. Auch hier ist zu beachten, dass die relativen Maße von der Auswahl der Benchmark-Methode abhängen und davon, wie gut die Zeitreihe mit der gewählten Methode vorhergesagt werden kann.
Nicht-Saisonal![]()
Saisonal![]()
SDMAE
Der Grundgedanke bei der Verwendung des MAPE zum Vergleich verschiedener Zeitreihen zwischen Prognosen ist meines Erachtens, dass derselbe absolute Fehler für Zeitreihen auf höheren Ebenen weniger problematisch ist als für Zeitreihen auf niedrigeren Ebenen. Anhand der zuvor gezeigten Beispiele denke ich, dass diese Idee zumindest fragwürdig ist.
Ich vertrete die Auffassung, dass die Bewertung eines bestimmten absoluten Fehlers nicht vom allgemeinen Niveau der Zeitreihe abhängen sollte, sondern von ihrer Variation. Dementsprechend ist das folgende Maß, der SDMAE (Standard Deviation adjusted Mean Absolute Error), ein Produkt der diskutierten Fragen und Überlegungen. Es kann zur Bewertung von Prognosen für Zeitreihen mit negativen Werten verwendet werden und leidet nicht darunter, dass die tatsächlichen Werte gleich Null oder besonders klein sind. Beachte, dass dieses Maß nicht für Zeitreihen definiert ist, die überhaupt nicht schwanken. Außerdem könnte es weitere Einschränkungen dieses Maßes geben, die mir derzeit nicht bekannt sind.
![]()
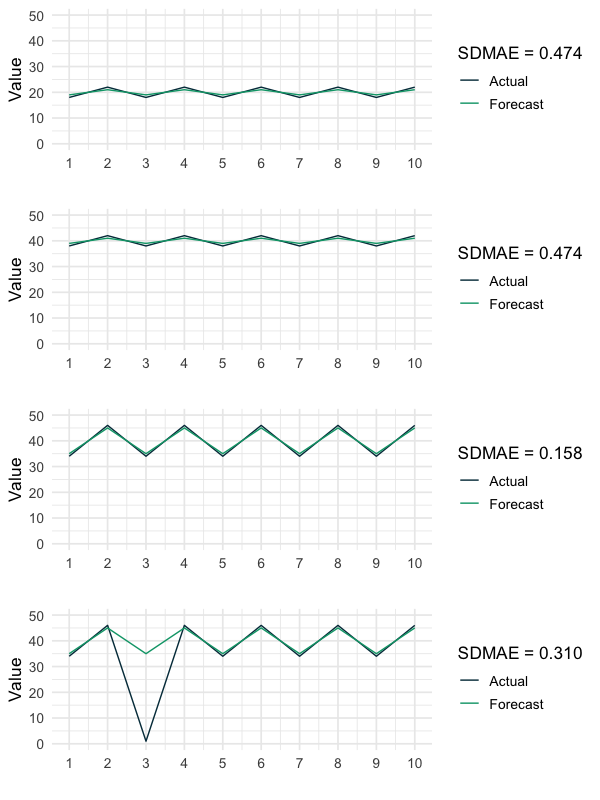
Zusammenfassung
Ich schlage vor, eine Kombination verschiedener Messgrößen zu verwenden, um ein umfassendes Bild von der Leistung der verschiedenen Prognosen zu erhalten. Ich empfehle außerdem, den MAPE durch eine Visualisierung der Zeitreihe, die die tatsächlichen und die prognostizierten Werte enthält, den MAE und einen Scaled Measure oder Scaled Error zu ergänzen. Der SDMAE sollte als alternativer Ansatz gesehen werden, der bisher noch nicht von einem breiteren Publikum diskutiert wurde. Ich bin dankbar für deine kritischen Gedanken und Kommentare zu dieser Idee.
Schlechtere Alternativen
SMAPE
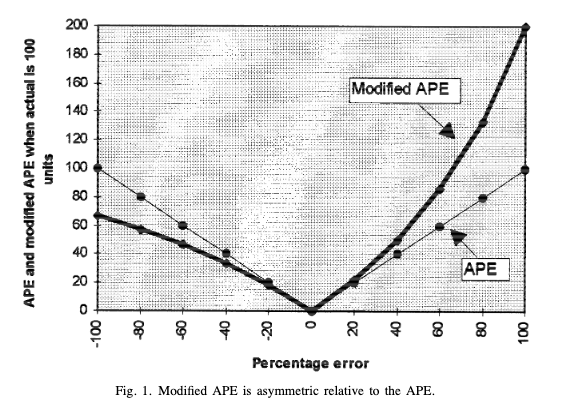
Der SMAPE wurde geschaffen, um die Probleme des MAPE zu lösen. Damit wurde jedoch weder das Problem der extrem kleinen Ist-Werte noch die Niveauabhängigkeit des MAPE gelöst. Der Grund dafür ist, dass extrem kleine tatsächliche Werte in der Regel mit extrem kleinen Vorhersagen verbunden sind *(Hyndman & Koehler 2006)*. Außerdem wirft der SMAPE im Gegensatz zum unveränderten MAPE das Problem der Asymmetrie auf *(Goodwin & Lawton 1999)*. Dies wird durch die folgende Grafik verdeutlicht, wobei sich der „APE“ auf den MAPE und der „SAPE“ auf den SMAPE bezieht. Sie zeigt, dass der SAPE bei positiven Fehlern höher ist als bei negativen Fehlern und daher asymmetrisch. Die SMAPE wird von einigen Wissenschaftlern nicht empfohlen (Hyndman & Koehler 2006).
![]()
On the asymmetry of the symmetric MAPE_ _(Goodwin & Lawton 1999)
Quellen
- Goodwin, P., & Lawton, R. (1999). On the asymmetry of the symmetric MAPE. *International journal of forecasting*, *15*(4), 405-408.
Hyndman, R. J., & Koehler, A. B. (2006). Another look at measures of forecast accuracy. *International journal of forecasting*, *22*(4), 679-688.
Makridakis, S. (1993). Accuracy measures: theoretical and practical concerns. *International Journal of Forecasting*, *9*(4), 527-529.
Armstrong, J. S., & Collopy, F. (1992). Error measures for generalizing about forecasting methods: Empirical comparisons. *International journal of forecasting*, *8*(1), 69-80.
